オームの法則とは何かわかりやすく説明してほしい!
こんにちは!この記事を書いているKenだよ。カーペット、2分割だね。
電気の分野で重要になってくるのが、
オームの法則。
オームの法則とは簡単に言ってしまうと、
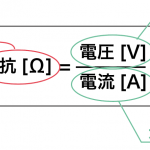
ある抵抗にかかる電圧・抵抗値・電流の関係を示した公式
のことだよ。
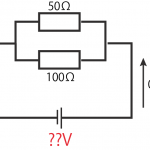
電圧・抵抗値・電流のどれか2つがわかっていれば、残りの1つがわかっちゃう、という魔法のような法則なんだ。
具体的にいうと、オームの法則の公式は
電圧 = 電流 × 抵抗
で、アルファベットで表すと(電圧をV、抵抗をR、電流をI)、
V = RI
になるね。

テストにオームの法則はめちゃくちゃでやすいから、まずは
オームの法則は一体何者なのか?
を説明していくよ。
オームの法則とは何か?
オームの法則とは、
抵抗器に流れる電流の大きさは両端にかかる電圧の大きさに比例する
という法則のこと。
つまり、ある抵抗に電圧を2倍かけたら、抵抗に流れる電流も2倍になるってわけ。

100倍の電圧をかけたら電流も100倍になるし、1000倍の電圧なら1000倍の電流が流れるのね。
物体ごとに「電流の流れやすさ」が違う・・・!
オームの法則の何が凄いかって言うと、
物体ごとに電流の流れやすさが違うってことが発見されたことかな。
例えば、3ボルトの電圧をかけた時、1アンペアの電流が流れる物体もあるし、

同じ3ボルトをかけても2アンペア流れる物体もあるってわけだ。

この流れる電流の違いは何なのか??
実はこれは、
物体ごとに電気抵抗という「電流の流れやすさが違う」からなんだ。
これを発見したのがオームの法則の最大の功績とも言えるね。

誰が発見したの?
この法則を発見したのはオームの法則の名前にもなっている「ゲオルク・オーム」っていうドイツの人。

https://upload.wikimedia.org/wikipedia/commons/d/dc/Ohm3.gifより
この物理学者が1826年に発見した法則なんだ。
彼は抵抗に電圧をかけていって、その時に流れる電流を計測してみたんだけど、
「電流が電圧の大きさに比例してるやん!」
って気づいてしまったんだね。
どこからオームの法則が出てきた?
電圧と電流は比例関係にあるから、
y = ax
という比例の式で表せる。
xは電圧、yは電流のこと。グラフで書くとこんな感じになるよ↓

比例だから原点(0, 0)を通っているし、直線のグラフになるはずだね。
比例定数をaとしてあげれば、
電流 = 比例定数a × 電圧
I = a V
という式が成り立つよ。
※電圧をV、電流をIとする

ここで、比例定数に注目。
こいつが大きければ大きいほど電流が流しやすく、小さければ小さいほど電流が流れにくくなるよね?
つまり、これは「電流の流れやすさ」を表しているんだ。
さっき紹介した電気抵抗とは逆のことだよね。

抵抗は大きければ大きいほど電流が流れにくくなるから、じつはこの比例定数aを逆数にした
a分の1
が抵抗Rのことになる。
つまり、
a = R分の1

だから、これをさっきの
電流 = 比例定数a × 電圧
に代入してあげると、

電流 = 比例定数a × 電圧
I = R分の1 × V
※ 抵抗をRとする
これをVについて等式変形してやると、
V = RI
という最初に紹介したオームの法則の公式になるわけだ。

さあ、オームの法則をガンガン使っていこう!
これがオームの法則の概要だね。

V = RI
公式を覚えるの大変かもしれないけど、本質さえ押さえておけば公式を忘れても大丈夫。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







ひゃああ!新しいの出てるう!久しぶりじゃないですかーー!!
明日中間テストなので、助かってます。ありがとうございます♪
ありがとう!!テストがんばれ〜
A,V,Ω,と I,V,Rってどう違うんですか…!?。゚(゚´ω`゚)゚。
A,V,Ωは単位で、I,V,Rは電流、電圧、抵抗を表す文字だよ!
はじめまして、物理初心者です。
グラフを作る過程のところで縦軸を電圧、横軸を電流とすると、
Ⅴ=1/R×Ⅰ
I =VR
になってしまわないのですか?
いつもありがとうございます
物理ダメダメです〜、、、
テスト頑張りますー!
がんばろうぜ!
法則って覚えると楽しいですよね~
僕中学受験するんですが先生が中学受験に役立つよと言ってたんですが本当ですか?
はじめまして!
オームの法則について、何か覚えやすい語呂合わせなどあったら教えてくれると助かります!
よろしくお願いします!
「オーム」を「オメガ」とよみがち。
なんかもっと分かりやすい覚え方無いですかね?