一次関数の利用で動点の問題がむずい??
こんにちは!この記事をかいているKenだよ。
一次関数の利用の問題ってムズい。
中でも、
動点の問題
が一番ヤッカイなんだ。たとえば、つぎのような問題だね。
タテの長さが4cm、横の長さが5cmの長方形ABCDの周上を、点Pは毎秒1cmの速さで、AからB、Cを通ってDまで移動します。
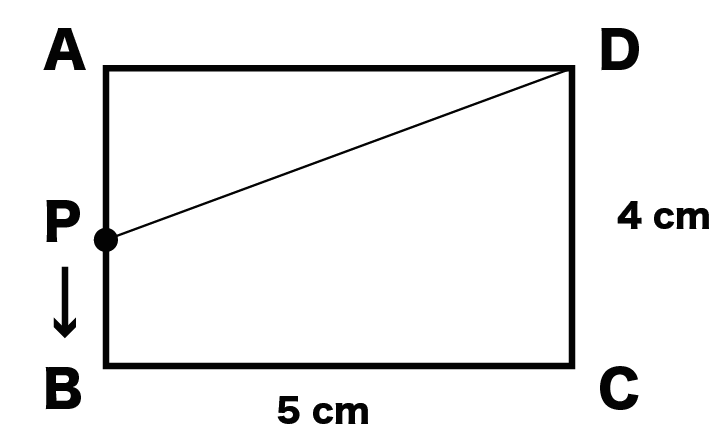
PがAを出発してからx秒後の△APDの面積をy cm²とするとき、yはxの変化にともなってどう変化するのか説明しなさい。
今日はこの動点の問題をわかりやすく解説していくよ。
よかったら参考にしてみてね^_^
一次関数の利用の「動点」問題がわかる3つのステップ
問題のポイントは、
三角形の高さだけが変化していること
だ。
逆に、底辺はどんなに時が経っても動かない。
高さの変化をトラッキングすれば面積が計算できそうだね。
例題でいうと、
△APDの底辺ADは固定だね?
だって、AとDは動かないからさ。
Pの移動によって高さだけ変わっていくんだ。
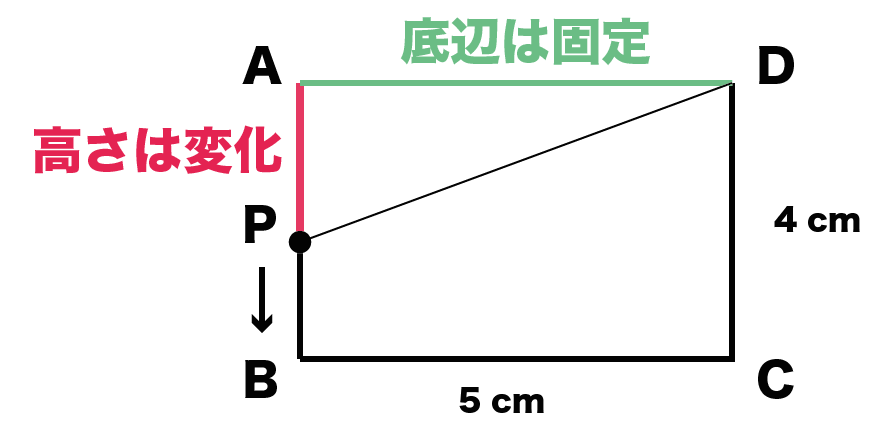
しかも、高さの変化は点が辺を移動するたびに変わっていくよ。
例題でいうと、動点Pが、
- 辺AB
- 辺BC
- 辺CD
にそれぞれあるときの3パターンだね。
今日はこの3つのフェーズごとに解説していくよ。
フェーズ1. 点Pが辺AB上を動いているとき
PがAB上を動いている場合だ。
このとき、△APDの高さは、
APの長さ
だよね??
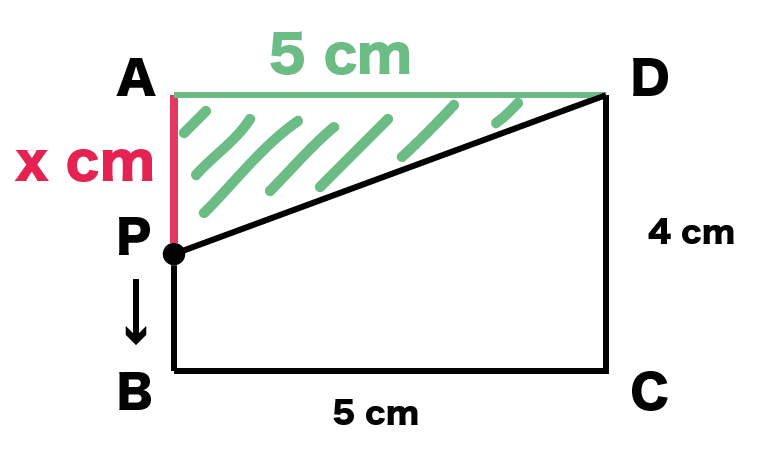
Pは1秒間にx cm動く。
APの長さはx秒後に「x cm」になっているはずだ。
よって、動点Pが辺AB上にあるとき(0 ≦ x ≦4)のとき、
△APDの面積は、
△APD = 底辺 × 高さ × 1/2
= 5 × x × 1/2
= 5/2 x
になるね。
ここまでの△APDの面積yの変化をグラフにしてみると、
こんな感じになる ↓↓
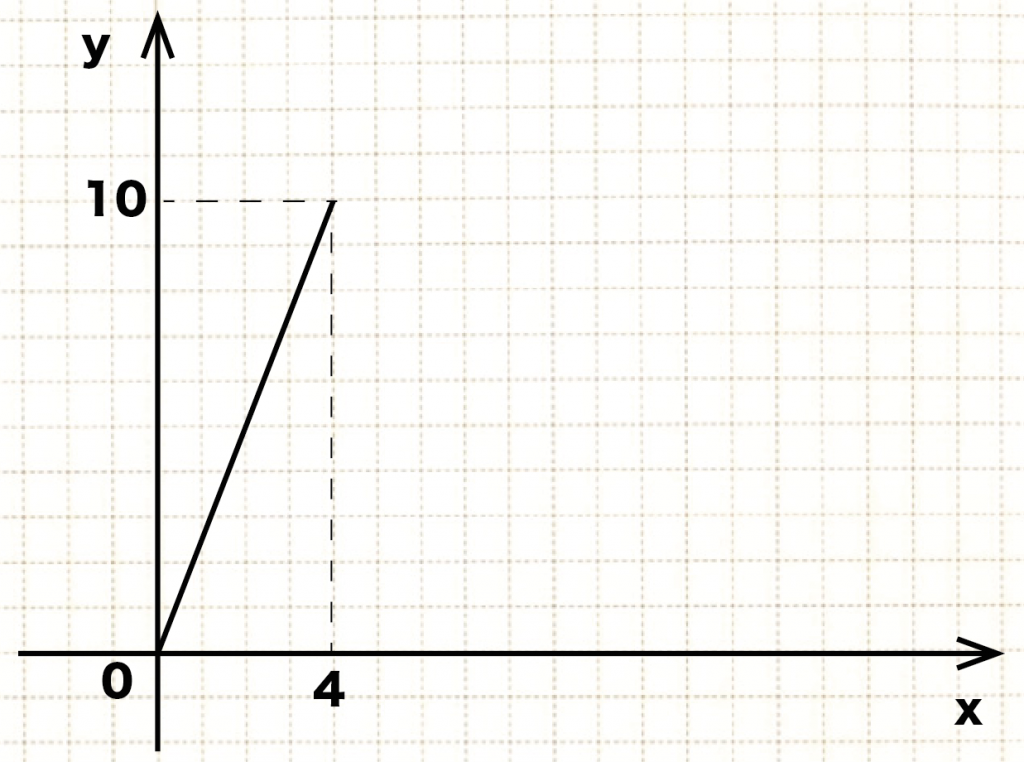
パターン2. 動点Pが辺BC上にある場合
つぎは点Pが辺BCにたどり着いたケース。
まだまだ動点Pの旅は続くんだ。辛いね。
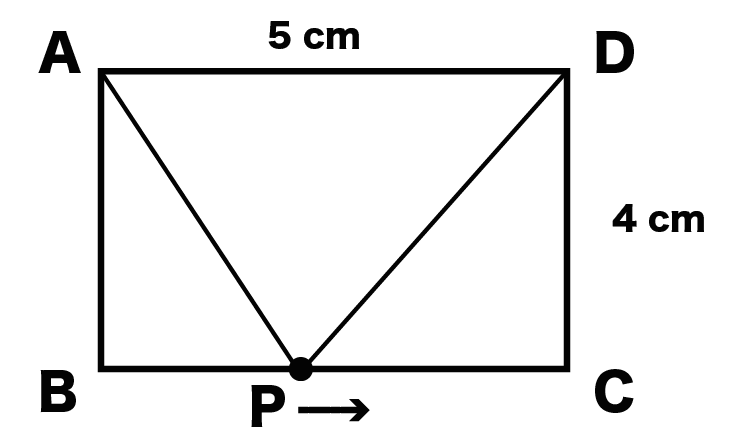
PがBC上にあるときの△APDの高さって、
点Pから辺ADにおろした垂線になるよね?
垂線とADの交点をHとすればPHが高さってことだ。
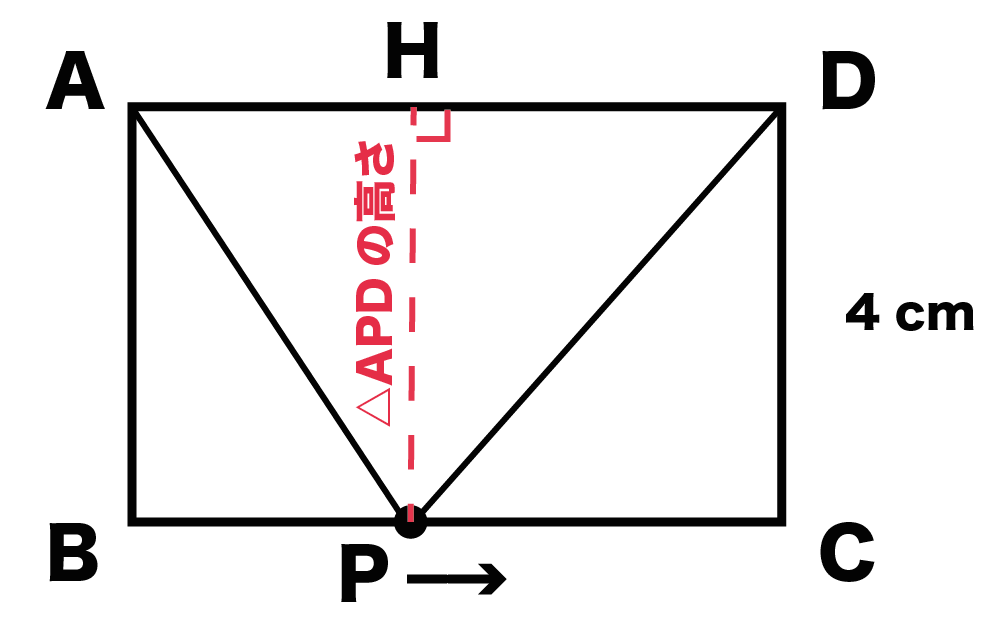
じつはこの高さって、
動点Pが左らへんにいても、
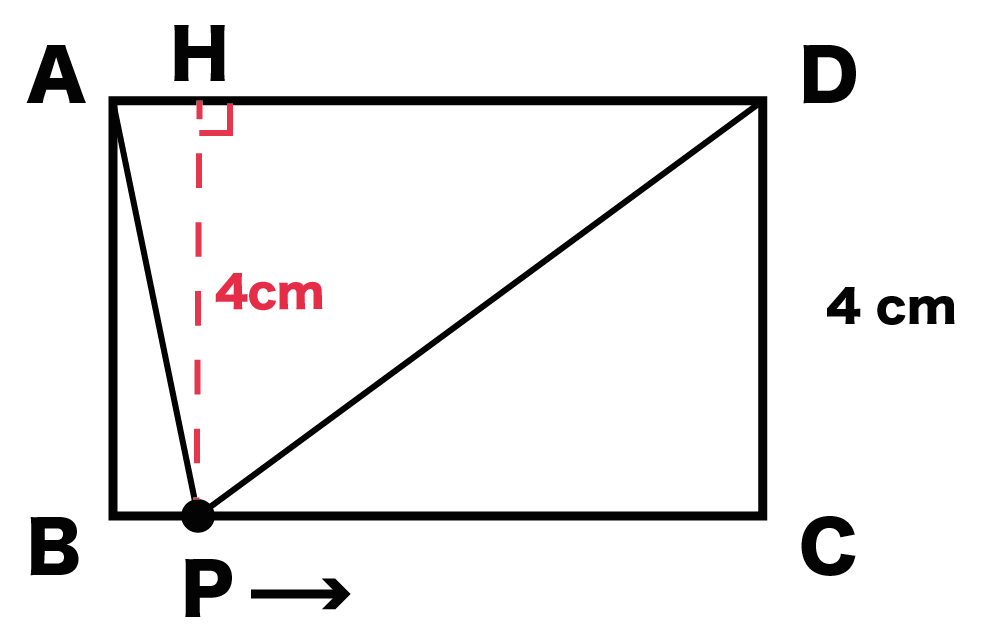
真ん中らへんにいても、
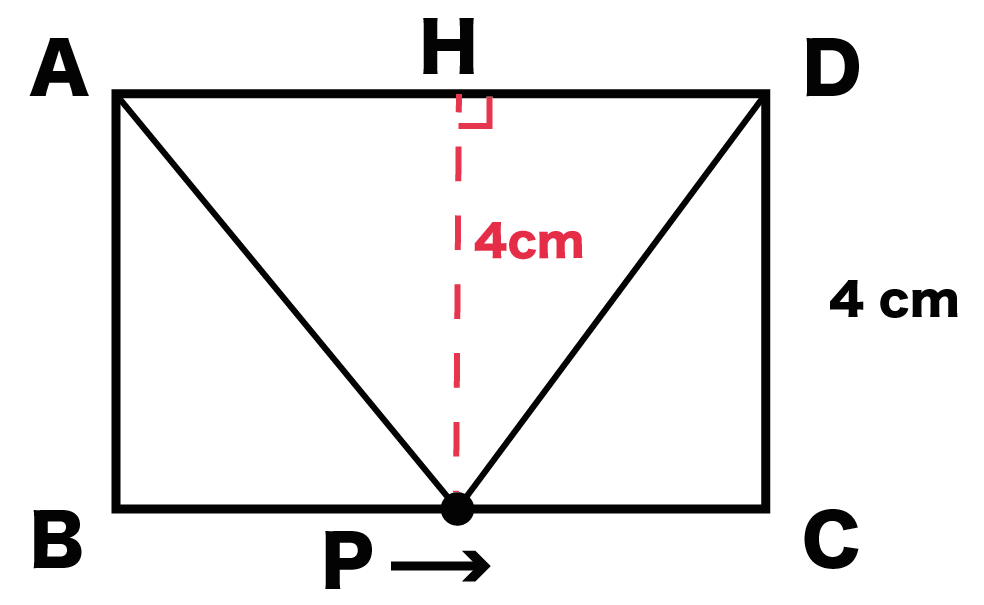
右のほうにいても、
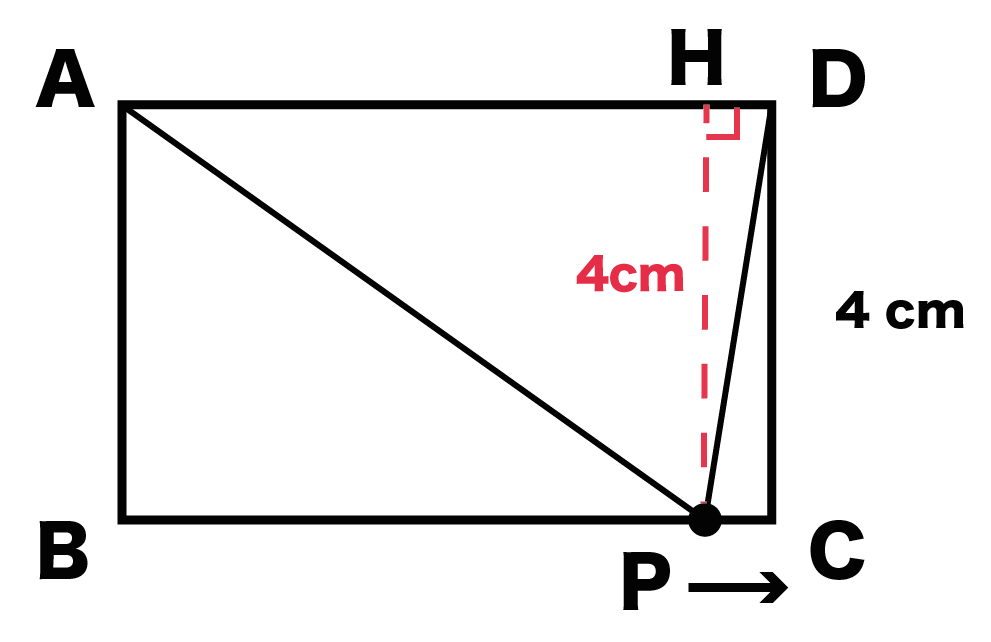
変わらないんだ!
ぜんぶ辺AB・DCと同じ長さ(4cm)になるはず。
よって、動点Pが辺BC上にあるとき(4 ≦ x ≦ 9)、
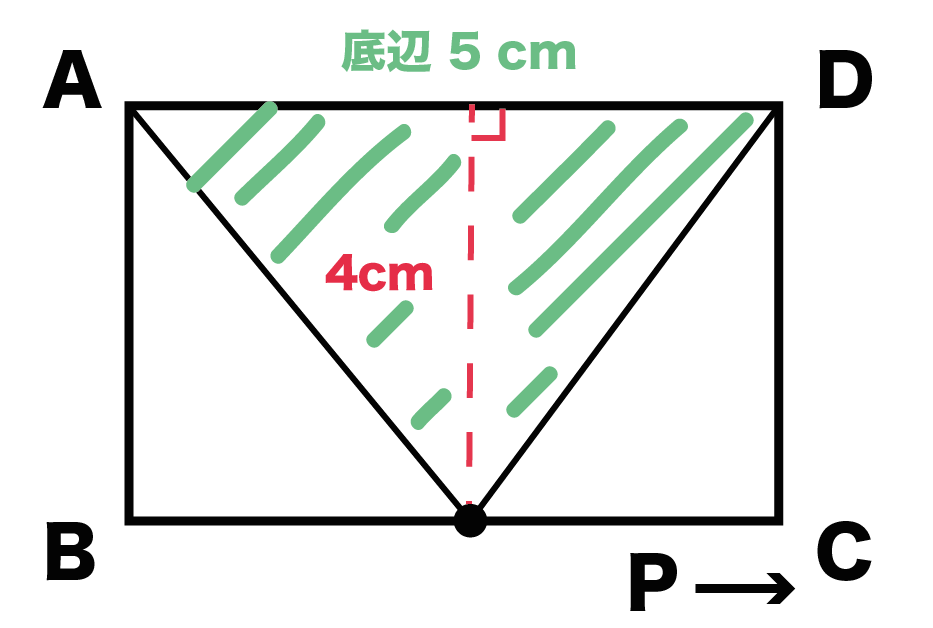
△APD の面積 = 底辺AD × 高さ × 1/2
= 5 × 4 × 1/2
= 10[cm²]
になるね。
つまり、動点PがBC上にあるとき、
△APDの面積はつねに一定というわけさ。
変数xがはいっていないからね。
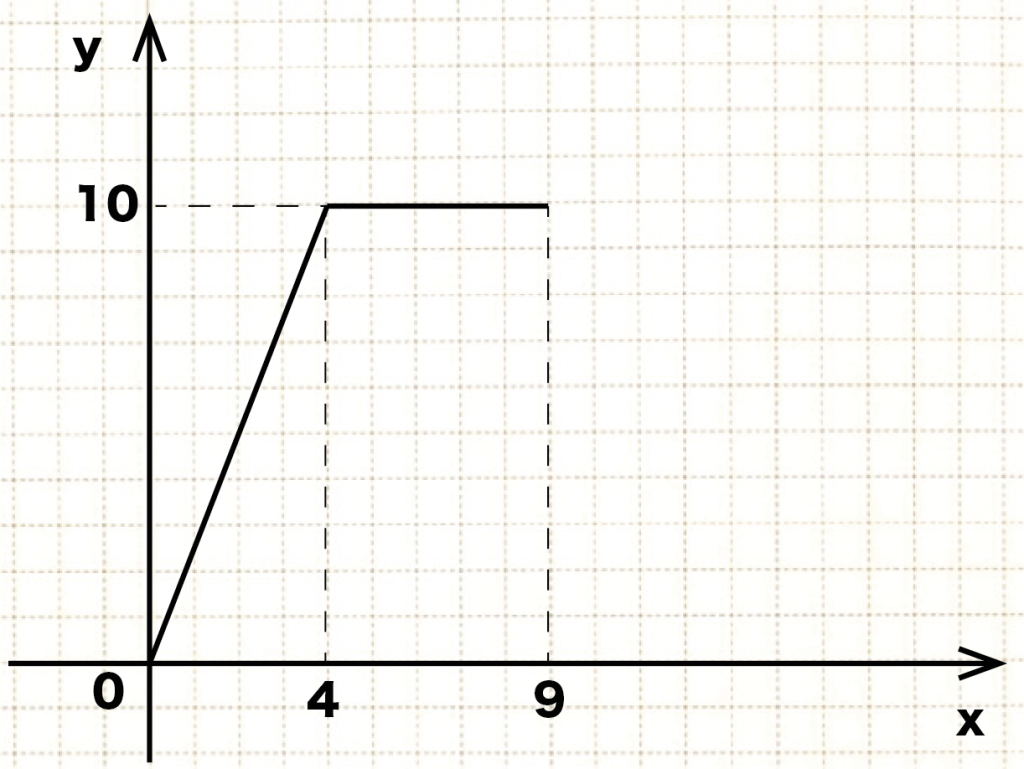
ここまで△APDの面積の変化をグラフにあらわすと、
こうなるね↓↓
フェーズ3. 動点Pが辺CDにある場合
いよいよ最後のフェーズ。
Pが辺CDにさしかかった場合さ。
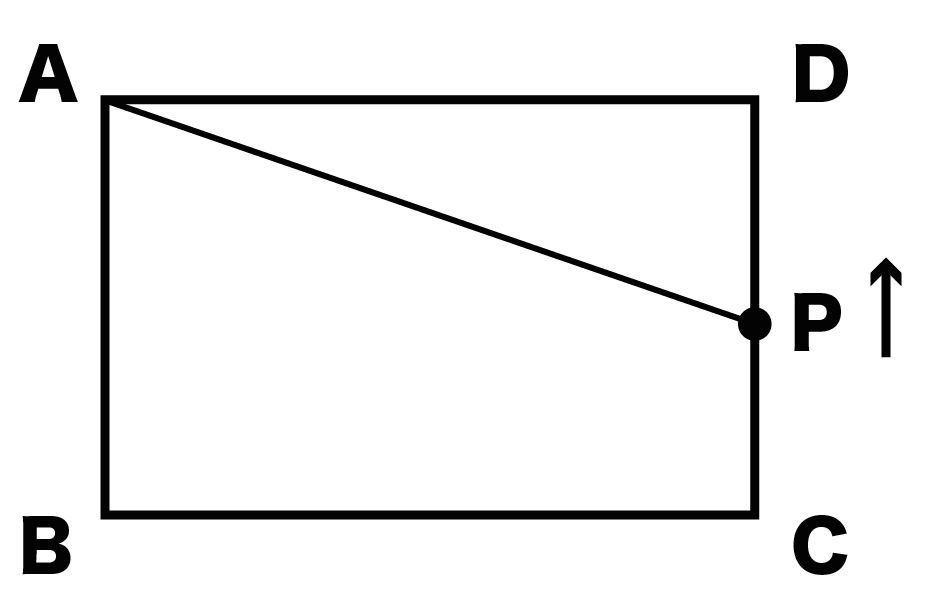
このときの△APDの高さって、
線分DPだよね?
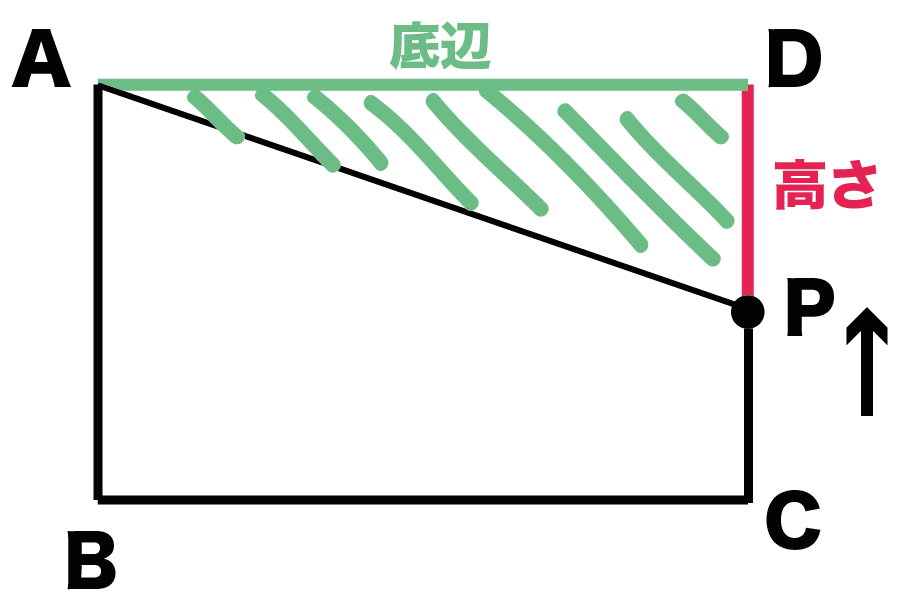
x秒後のDPの長さをだしてやれば、
△APDの面積yを式であらわせるってこさ。
このときの高さDPは、
「3つの辺(AB・BC・CD)」 – 「 Pが動いた距離」
で計算できるよ。
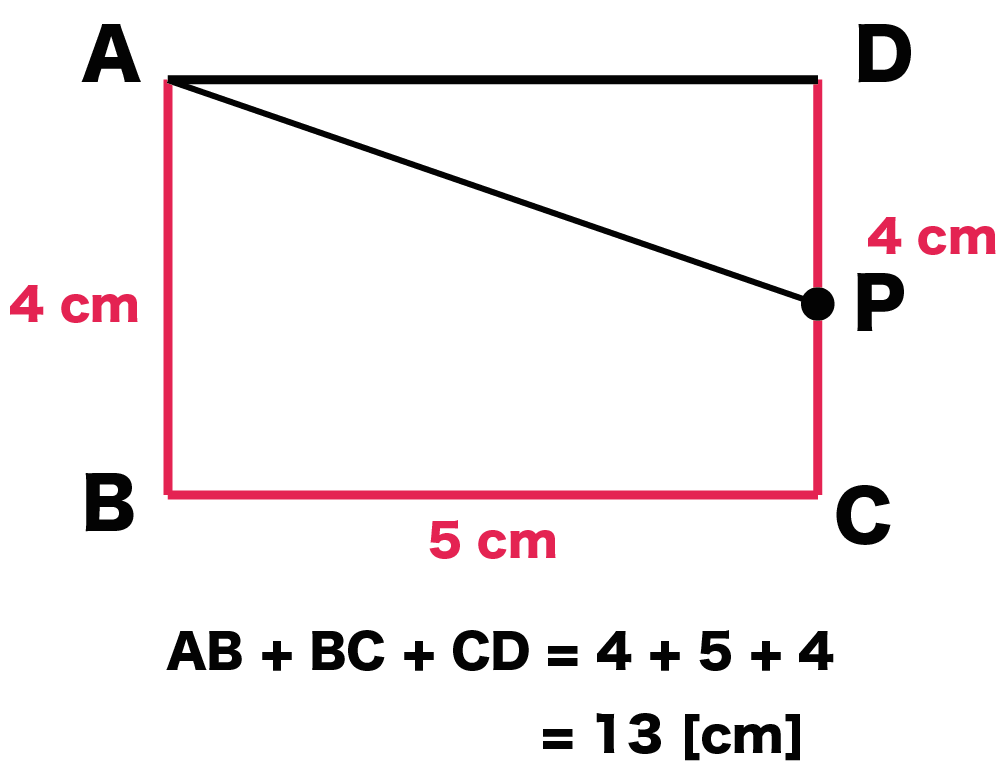
(3つの辺の長さ)= 4 + 5 + 4
= 13 [cm]
になる。
そんで、x秒後に「Pが動いた距離」は、
x [cm]
だね。
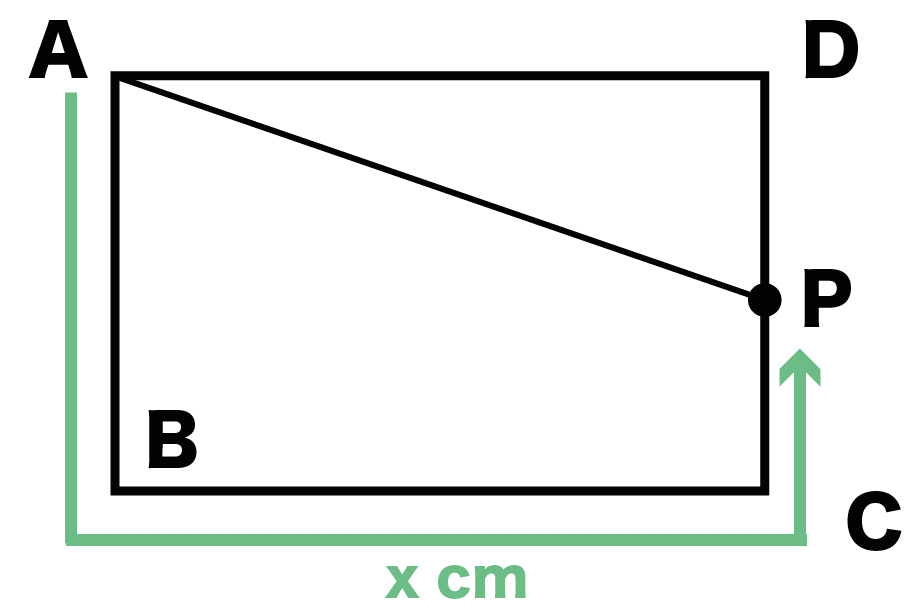
ってことで、
DPの長さは(3つの辺の長さ)- (Pが動いた距離)で求めることができるので、
13 – x
になるね。
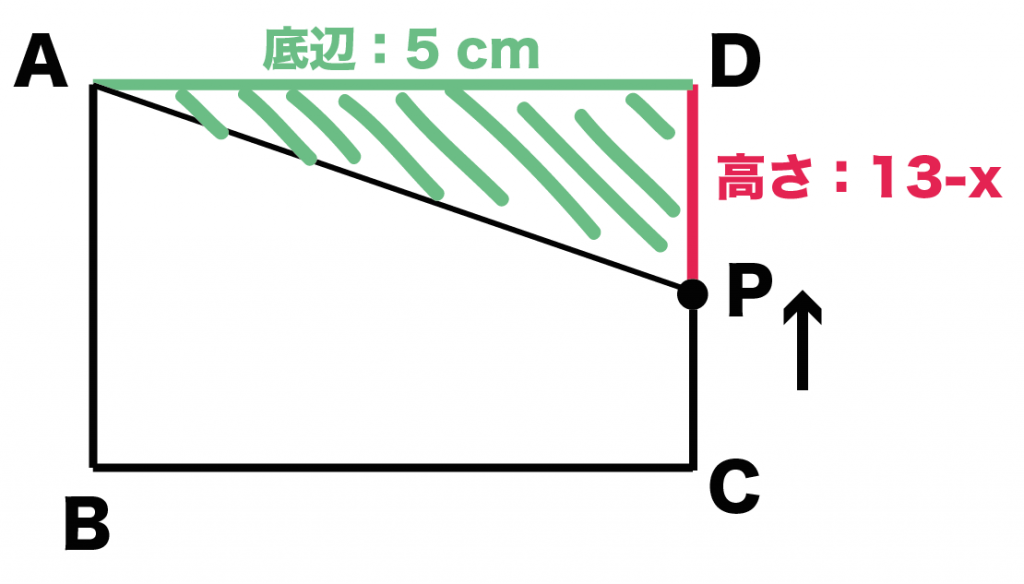
よって、Pが辺CD上を動くとき(9 ≦ x ≦ 13)、
△APDの面積 = 底辺AD × 高さDP × 1/2
= 5 × (13-x) × 1/2
= 5/2 (13-x)
となる。
よって、こいつをグラフに表してやると、
こうなるね↓↓
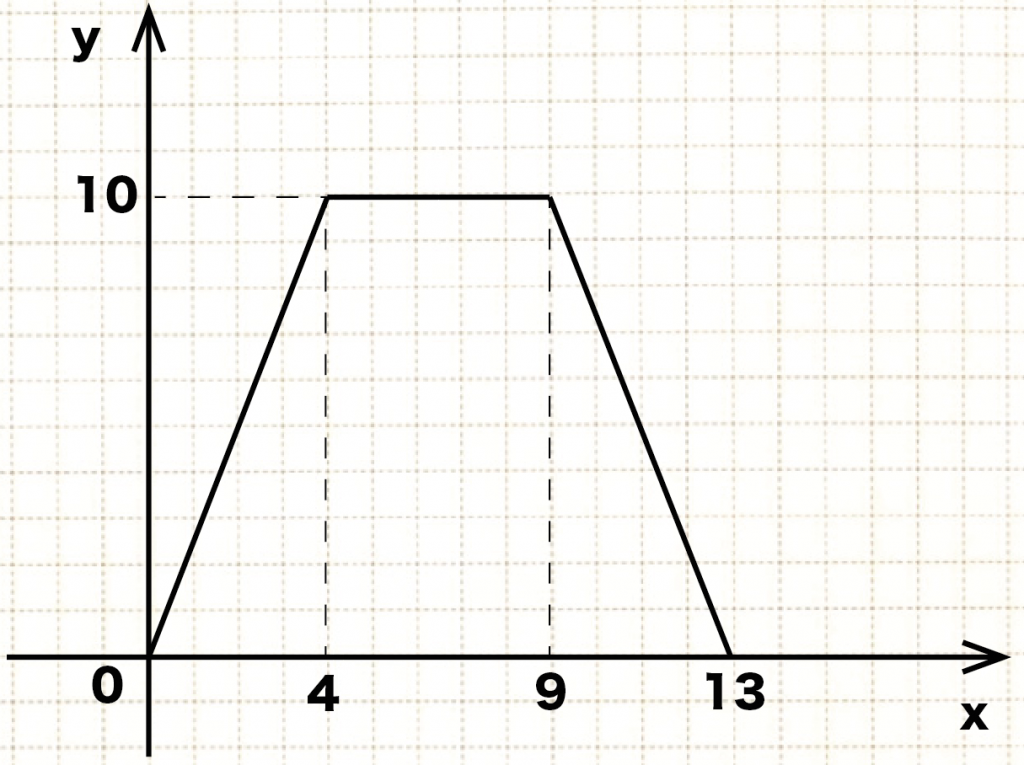
△APDの面積yをxであらわすことができて、
それをグラフにすれば完ぺきだ!
テストに出やすい問題だからしっかりおさえておこう^^
まとめ:一次関数の利用の動点は3つのフェーズにわけるべし
動点の問題はどうだった?
フェーズごとに面積の変化が異なる
ってことさえ押さえておけば十分さ。
あとは、
どの辺が底辺・高さになっているのか??
ということに注意してみてね。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






動点OとQの問題がわからないです
問題文送ってみて!
ここの問題とても苦手でしたがとてもわかりやすく少しわかるようになりました!ありがとうございます
ありがとう!!この調子で行こう!!
とても分かりやすかったです!ありがとうございます!
ありがとう!励みになるぜ!
すごくわかりやすいです!!
一次関数すごく苦手なので、頑張ります!!
ありがとう!!一次関数制覇しようね!!
「グラフ上に直線が二本あって交点をP、それでこのPが直線上を動く。△TOPを求めよ。」
教えてください。
>グラフ上に直線が二本あって交点をP、それでこのPが直線上を動く。△TOPを求めよ。
TとOがなんなのかわからん!
変域がよく分からないです…
「変域」に関する記事を読んでみて
質問なんですけどOP=pのOPの意味がわかりません
三角形のときはどーすれば。
身のまわりの一次関数が分かりません
問題送ってみて!
動点ムズイです
数学はどうしたら得意になりますか?
三角形が三角形の中を移動するときの
一次関数の利用はどうすれば解けますか?
教えてください!!お願いします。
動点の問題は、点が辺をうつるフェーズごとに図をかいて整理すればいいね
>数学はどうしたら得意になりますか?
数学に限らずだけど、インプットとアウトプットの総量が物を言うね。
教科書を読んで基礎を習得したら、それを使って問題をたくさん解いてみよう。
あとは間違えた問題を復習して同じ失敗を二度繰り返さないようにしよう
>三角形が三角形の中を移動するときの
一次関数の利用はどうすれば解けますか?
パターンが変わっても解き方はだいたい一緒じゃないかな。
面積が変化の仕方が変わるxの変域をいくつか区切ってやって、それぞれの面積をxで表してみよう
なぜ、図を書くやつでxが4になるのはわかるんですけど、10になるのはなぜんなですか?
教えてください
それと、なぜ最後13の所が0になるんですか?
>なぜ、図を書くやつでxが4になるのはわかるんですけど、10になるのはなぜんなですか?
教えてください
それと、なぜ最後13の所が0になるんですか?
xはPが動いた距離だったよね?
だから、xが13になるのは点Dに到達した時で、その時は三角形ADPの面積は0だ
点pが辺CD上を頂点Cから頂点Dまで移動するときのXの変域を求めなさい。
また、このときのxとyの関係を式に表しなさい。
というのがわかりません。変域まではわかるのですが式になると、、
(図形は縦6センチ 横が8センチの長方形です。毎秒2センチで動きます。
ABCDの並びはkenさんが解説したときの並びと一緒です。)
教えてくれると嬉しいです。
>点pが辺CD上を頂点Cから頂点Dまで移動するときのXの変域を求めなさい。
また、このときのxとyの関係を式に表しなさい。
xの変域は、xがCに到達するときから、Dにたどり着くまでの時間を変域にすればいいね。
毎秒2cmで動いてるから単純に辺の長さにはならない点に注意してね
yは△APDの面積かな?こいつはDPの長さが高さになるから、DPをxで表してみよう!
ポイントは、Pが進んできた道のりは2xcmだということかな
お忙しいところすいません
追加で質問したいです。答えでは
y=-80x+80となるのですが
なぜxの係数がー80になるのですか?
>y=-80x+80となるのですが
なぜxの係数がー80になるのですか?
xの係数はその時の面積の変化具合によって異なるかな。
係数がマイナスってことは、時間がたつと面積が小さくなるってことだ
ありがとうございました。 お陰で理解できました。
発展的な問題もガンバリマス!
またわからないところがあったら宜しくお願い致します。
おお!がんばろうぜ!!
とても分かりやすかったです!!
授業で全然分からなくて悩んでいたところです。ありがとうございます
よかった!!^^ 頑張ろうぜ!
これ、台形の時も同じようにとけますか?
三角形でなく、四角形の動点の問題がわからないです
とけるはず!
>三角形でなく、四角形の動点の問題がわからないです
基本は一緒だね!
四角形だと2つの三角形に分けて考えたほうがいいかも
”面積が〇cmになるのは点PがAを出発してから何秒後ですか、すべて答えよ”
という問題がでたらどう解けばいいですか?
>”面積が〇cmになるのは点PがAを出発してから何秒後ですか、すべて答えよ”
という問題がでたらどう解けばいいですか?
面積がyだとしたら、その〇を一次関数のyに代入して、
その時のxを求めればいいね
動く点Pの、台形バージョンは、どうやって解くことができますか?
テストの時のアドバイスを教えてください!
メッチャわかりやすくてよかったです
>動く点Pの、台形バージョンは、どうやって解くことができますか?
台形でも基本は同じ。
三角形の面積は「底辺x高さ」で求められるから、
x秒後の底辺と高さをxで表せばいいんだね!
>テストの時のアドバイスを教えてください!
難しい問題に時間を取られないことも大事。
まずは確実に点が取れる基礎問題をミスなくこなしてから、応用問題に取り組むといいよ
ありがとう!!
今回は三角形だったのですが問題で2点P,Qの動く台形が出て、台形の場合はどう解けばいいでしょうか?
わかりやすい!
わかりやすかったです!
全然わからなくて困ってたんですけど
これ見たら大丈夫そうになってきました!
ありがとう!!動点倒そうぜ!
一次関数の利用がわかりません。
直角三角形ABCがあり、PはAから出発して、毎秒1センチの速さで、周上をCを通ってBまで移動します。CA=4㎝CB=2㎝DはAB上の点で、AD=3㎝です。PがAを出発してからBまで移動する間に、三角形PADの面積1センチ㎡ 以上になるのは何秒間ですか。
>直角三角形ABCがあり、PはAから出発して、毎秒1センチの速さで、周上をCを通ってBまで移動します。CA=4㎝CB=2㎝DはAB上の点で、AD=3㎝です。PがAを出発してからBまで移動する間に、三角形PADの面積1センチ㎡ 以上になるのは何秒間ですか。
三角形の面積は底辺と高さが分かっていれば求められるね。
DからACに推薦を下ろして交点をHとし、高さを出してみよう!
すげーマジ神!
このような動点の問題、サッパリ分からなくて苦戦していたんですけれど、この解説(?)を見たら解けるようになりました! 本当にありがとうございました(__)
ありがとう!!動点を倒そうぜ!
すごく分かりやすい説明ありがとうございます!!
今年受験生で、一次関数すごく苦手でしたが
説明のおかげで分かるようになりました!
ありがとう!一度わかってしまえば動点はこっちのものだね!
点Pが秒速2cmでは、Pは1秒間に2cm動く。
すなわちAPの長さはx秒後に2xcmになるということですか?
>点Pが秒速2cmでは、Pは1秒間に2cm動く。
すなわちAPの長さはx秒後に2xcmになるということですか?
その通り!
テストに出るって授業でいわれて焦っていたのですが、いけそうです!
ありがとうございました
よかった!動点で得点取って行こうぜ!
今まで、ずっと動点問題のプロセスが無理解だったため、敬遠していましたが、この記事のおかげで理解ができました。本当にありがとうございます。
ありがとう!!動点を得点源にしちゃおうぜ
台形の場合はどうすればいいのですか?
やっと良いやり方にたどり着けました❗本当に本当にありがとうございます。学校より分かりましたすごいです。
おお!よかった!!
とても分かりやすくて、助かりました❗
逆に面積は分かっていて秒を求めたい時
はどうしたらいいですか?
等式変形して
秒=
の形にしてやるといいよ
正方形になっても同じ考え方で解けばいいんですか?ちなみに明日数学の単元テストがあります…
そうだね!正方形でも同じだ!
一次関数の利用が分かりません。
長方形ABCDで、点Mは辺CDの中点である。点Pは、毎秒1cmの速さで、辺AB、BC上をAからCまで動く。点PがAを出発してからx秒後の△APMの面積をycmとする。4≦x≦9のとき、yをxで表しなさい。
長方形は縦4cm、横5cmで、頂点は、左上がA、左下がB、右下がC、右上がDです!
長方形でも解き方は同じ!
1. PがAB上にある時
2. PがBC上にある時
3. PがDC上にある時
の3パターンの時のAPMの面積yをxで表してみよう。
APMは三角形だから、底辺と高ささえわかれば面積を計算できるね
質問です。
AB=6cm BC=4cmの直角三角形ABCがあり 点Pは毎秒1cmの速さで A→B→C と動く。
点PがAを出発してからx秒後の△ABPの面積をyとする。
6≦x≦10の時のyをxの式で表せ。
という問題で、なぜy=3x+10となるのか教えてください。
BPの長さをxで表して、そいつに高さABをかけて半分にすりゃいいね
なぜ(4不等号x不等号9)になるのですか?
パターン2の動点Pが辺BC上にある場合の変域です
不等号の記号が使えず、
わかりずらくてすいません…
>なぜ(4不等号x不等号9)になるのですか?
パターン2の動点Pが辺BC上にある場合の変域です
BC上ってことは、
PがBの上に来た時から、PがCにたどり着くまでの間ってことだ。
で、PがBにくるのはAからスタートして4秒後。なぜならPは毎秒1cmの速さで進んでいて、ABは4cmだからね。
PがCにくる時も同じ考えでAからCまでは9cmだから9秒後になる
今更なんですがとても分かりやすかったです……!!!
私の数学の先生問題の作り方もミスったらしくて中間で動点のお話終わったのに期末にも出てきまして……(´;ω;`)
中間のときボロボロでしたが今回はいけそうです!!
ありがとうございました……!!
先生は意図的に間違えてるかもね!笑
それほどこの問題は出やすいからマスターしておこう!
面積が10cm2になるのは何秒後か、という問題の求め方がわかりません。
面積がyの場合、y=10を関数に代入してxを求めればオッケー。
ただ、もしかしたら複数の領域で10cm2になるかもしれないから、そこはグラフを書くとわかりやすいかな。
学校で身の回りの動点についてレポートをかいてきなさいと、言われたのですがどうすればいいか分かりません!助けてください!!!(´TωT`)
これ身の回りにあるのかな笑
身の回りの一次関数ならありそうだけど!
なぜ3つの辺からPの距離を引くのですか?
すいません‥
こんにちは。少しわからないところがあるんですけどなぜ最後の問題で3つの辺を足してからP の動いた距離を引かなければ行けないんですか?
三角形の高さをxで表すためかな!
yをXの式で表すのはどうやってやるのですか?
それと、X、yのそれぞれの変域のやり方を教えてください!
とりあえず気軽に等式を作ればいいな!
そしてその後、y=にする
AB=3㎝、BC=4㎝である長方形ABCDの周上を、頂点Aから毎秒1㎝の速さで、点Dを通り点Cまで動く点Pがある。Pが頂点を出発してからx秒後の四角形ABCPの面積をy㎠とする。
⑴x=0以上4以下のとき、yをxの式で表しなさい。
⑵x=4以上7以下のとき、yをxの式で表しなさい。
⑶x=0以上7以下のときのxとyの関係を表すグラフを書きなさい。
⑷y=8になるxの値を全て求めなさい。
学校の数学の授業で出された問題なのですが‥‥ 分からなくて‥
教えて頂けませんか?
正方形ABCD で点P はaを出発して秒速2cm の速さで辺上をBC を通ってD まで動く。点P がA を出発してからX 秒後の▲PDA の面積をY cm とするとき ▲PDA の面積が12cm になるには点P がA を出発してから何秒後か求めなさい。という問題があるんですがわかりません。教えて頂けませんか?お願いします‼
やっほーです!kenさん、質問があります。。。。
この問題を教えて下さいm(_ _)m
長方形ABCDで、点PはAを出発して毎秒1cmの速さで、辺上をB、Cを通ってDまで動く。
点PがAを出発してからx秒後の△APDの面積をy cm二乗とする。yをxの式で表しなさい。
yをxの式で表せという問題がだされた後にxとyを表すグラフを書けと言われた場合の
グラフの書き方を教えてほしいです
よくわかりました!ありがとうございました!
めっちゃ分かりやすい‼︎
受験に出そう…汗
ぜんぜんわからん、、、
分からん
分からない
バナナはおやつに入りますか?
うーん・・・
よく理解できました!!これで中間の動く点P点取れます!有難うございます
すごいわかりやすかったです!!
ありがとうございます!
BからCを動く分には式にXはいらないのですが、面積をXの式で表せという問題があります。どうしたらよいでしょう。
娘の勉強を教えていて
点P動くなよおおおおとか思ってたところだったので
助かりました(笑)ありがとうございます
おかげで娘にいい顔出来ました
動点だけまったくできなかったけどこの記事みたらすぐできるようになりました!ありがとうございます!