【超簡単】平方根の求め方がわかる3つのステップ

平方根の求め方・出し方を知りたい！！

こんにちは！この記事をかいているKenだよ。スタミナを補給したね。

平方根の求め方にはいろいろある。

小数の平方根の求め方、

分数の平方根の出し方、

平方根を簡単にする方法・・・・

などなど。

まさに多種多様。

混乱しちゃうかもしれないね。

そこで今日は、

超基本的な平方根の求め方を解説していくよ。

いちばん簡単な求め方だから、

ガッツリおさえちゃおう！

平方根の簡単な求め方がわかる3ステップ

平方根の出し方を紹介するよ。

3ステップで求められちゃうんだ。

1. ルートをかぶせる
2. ±をつける
3. ルートをはずせたらはずす

つぎの問題をといてみよう！

例題

つぎの数の平方根を求めなさい。

7, 9

Step1. ルート（根号）をかぶせる

元の数にルートをかぶせよう。

そう、

√

をね。

ぱさっとね、上からかければいいんだ。

さっきの例題では、

• 7
• 9

の平方根を求めるんだったね？？

だから、こいつらの上に「√」をかぶせればいいのさ。

帽子みたいにね。

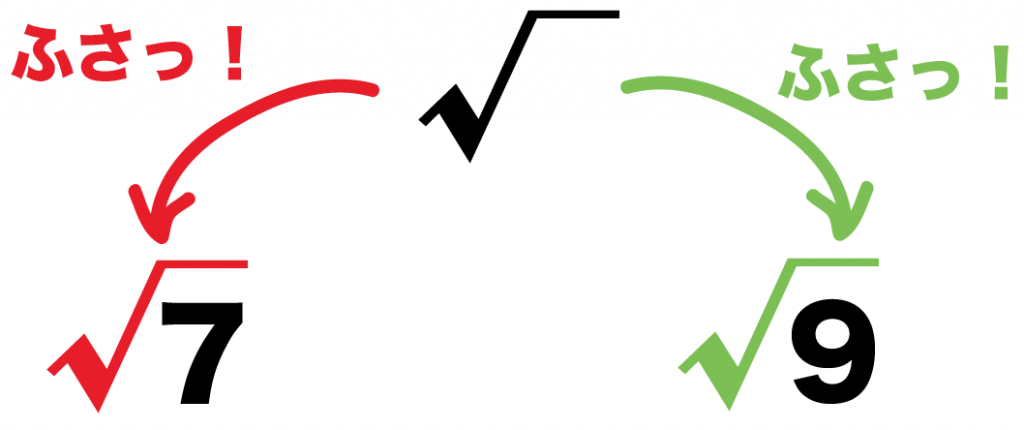
そうすると、

• √7
• √9

になるはずだ！！

Step2. ±をつける！

つぎは、

±（プラスマイナス）

をつけてやろう。

文字通り、

プラスとマイナスが合体した記号

だ。

平方根にはプラスとマイナスのものがあって、

どちらも絶対値が等しい。

だから、

プラスマイナスで1つにまとめられるんだ。

※くわしくは平方根の性質をよんでみてね。

例題でも、さっきルートをつけた、

• √7
• √9

に±（プラスマイナス）をつけよう。

付け方はくそ簡単。

ふつーに左にチョコっとくっつけるんだ。

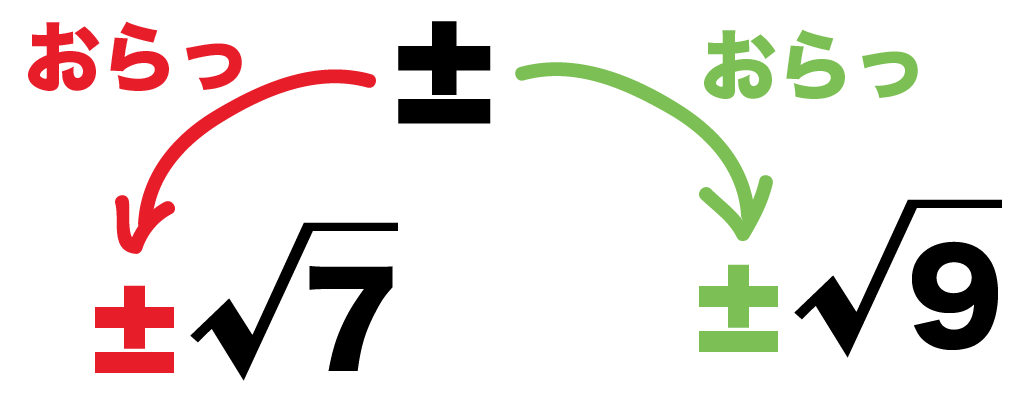
そうすると、

• ±√7
• ±√9

になるよね。

Step3. ルートをはずせたらはずす

せっかくルートをつけたんだけど、

ルートをもう一回はずせるかチャレンジしてみよう。

ルートをはずせる条件は1つ。

それは、

ルートの中身が「○○の2乗」になっていればいいんだ。

条件にあてはまるなら、

2乗とルートをとっていいんだ。

たとえば、±ルートaの2乗だったら、±aになるってわけさ！

例題を振り返ってみよう。

まず、±√7だ。

ルートの中身は7だね。

この中身の7は・・・・うーん、どうやっても、○○の2乗の形になおせない。

だって、2回かけて7になる整数なんてないし・・・！

だから、

±√7は±√7でいいわけだ。

あともう1つの±√9。

こいつはルートをはずせそうだ。

なぜなら、

ルートの中身の「9」が「3の2乗」になってるからね！

√をとってやると、

±√9 = ±3

になるってわけさ。

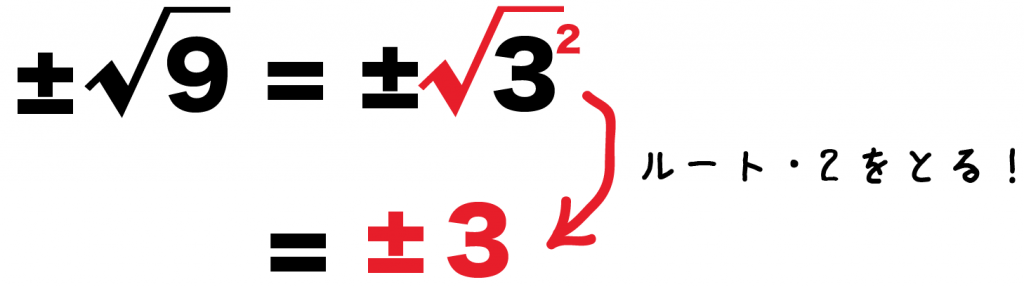
よって、

7と9の平方根は、

• ±√7
• ±3

の2つだ。

これで平方根の求め方もマスターだ！^-^

まとめ：平方根の求め方は√と±つければとりえあずOK

平方根の求め方はむちゃくちゃ簡単。

ルートをかぶせて、±を左にくっつける。

最後にルートをはずせるかトライするだけ。

ガンガン平方根を求めていこう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。