【中学数学】二等辺三角形の書き方・作図がわかる3ステップ

二等辺三角形の書き方・作図がわからない！？

こんにちは！この記事をかいているKenだよ。筆箱ほしいね。

二等辺三角形の作図問題ってたまにでる。

こんな感じのやつね↓↓

例題

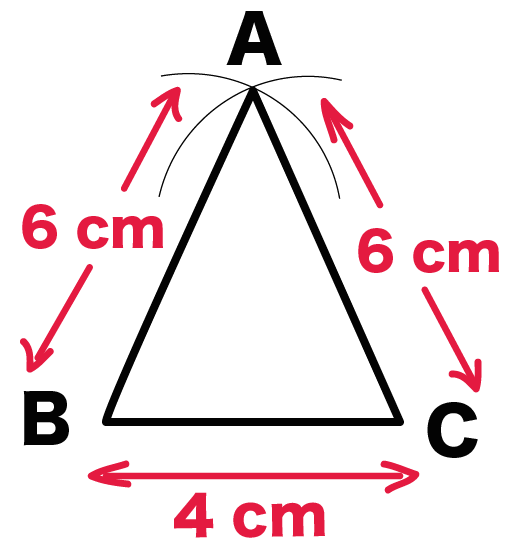
AB = AC = 6 cm、BC = 4cmの二等辺三角形ABCを作図しなさい。

この問題はぶっちゃけめんどい。

作図はセンスとわれそうだし、

コンパス使わなきゃいけないし。。

今日はそんな問題を瞬殺するために、

二等辺三角形の書き方・作図方法を3ステップで解説していくよ。

よかったら参考にしてみて^^

二等辺三角形の書き方・作図の3つのステップ

作図で用意するものは、

• コンパス
• 定規

の2つ。

これで作図できちゃうんだ。

例題をといてみよう。

例題

AB = AC = 6 cm、BC = 4cmの二等辺三角形ABCを作図しなさい。

Step1. 底辺をかく！

二等辺三角形の「底辺」をかこう。

使うのは、

定規。

きみだけだ。

定規で、

底辺の長さの直線をひけばいいんだ。

例の底辺の長さは、

4cm

だね？？

だから定規で、

すーーーっと4cmの底辺BCをひいてあげよう。

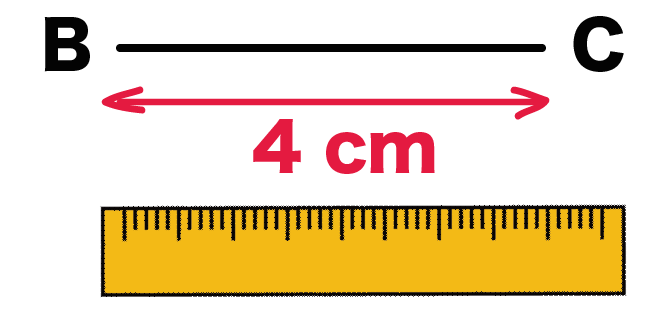
これが第1ステップさ！

Step2.  チョビ円をかく！

つぎはコンパスを使うよ。

こいつをつかって、

ちょびっと円をかいてみよう！

円の中心は「底辺の両端」、

半径は「底辺以外の辺の長さ」にするよ。

例題では、

底辺以外の長さは6cmだったよね？？

だから、

まずコンパスの脚を6cmに広げてみよう。

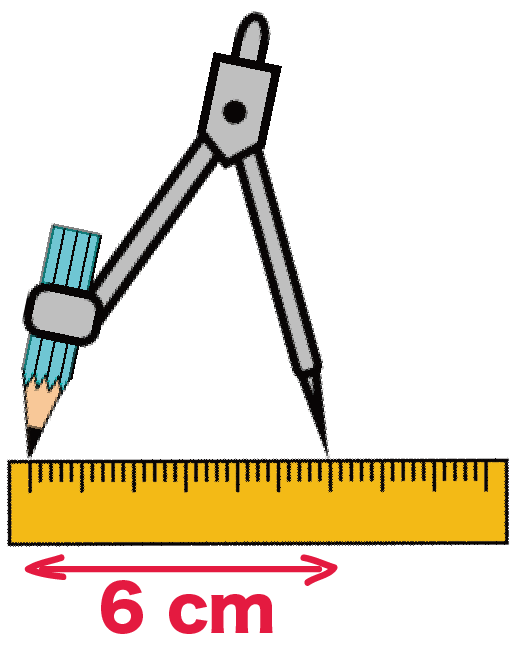
脚を6 cmにひろげたままで、

コンパスの針を頂点Cにもってきて。

んで、

ちょっと円をかいてみるんだ。

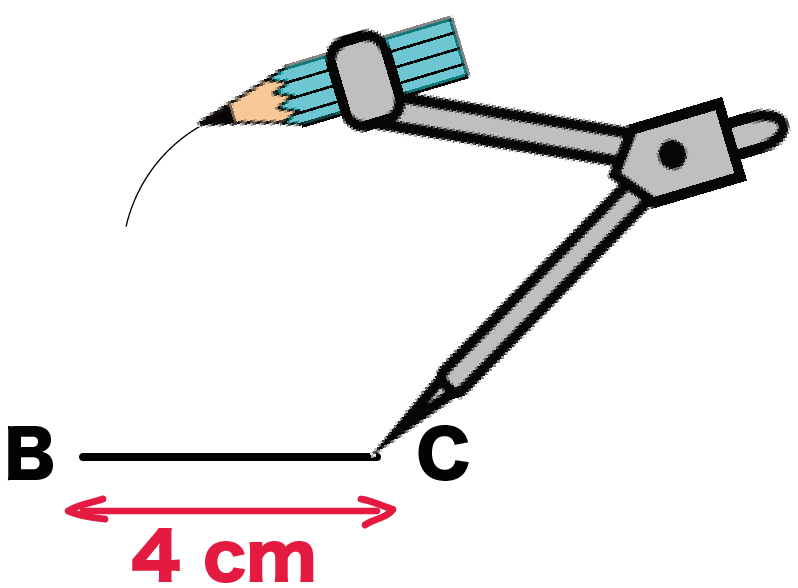
チョビ円のできありさ。

あとは同じことを点Bでもやるんだ。

つまり、

コンパスの脚を6 cmにひらいたまま、

点Bを中心にチョビ円をかくってこと。

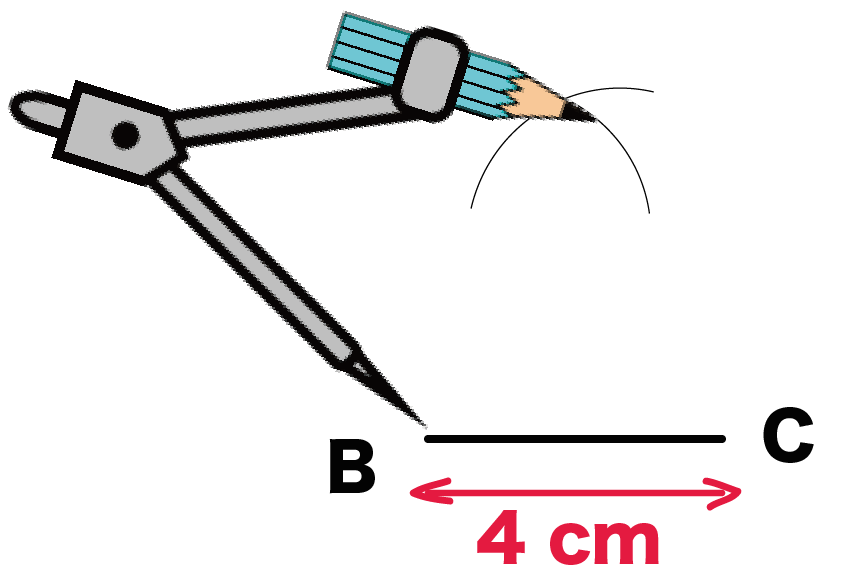
チョビ円がふたつできればオーケー。

第2ステップ終了さ。

Step3. 「チョビ円の交点」と「底辺の両端」をむすぶ！

「チョビ円の交点」と「底辺の両端」をむすぼう！

チョビ円の交点をAとするよ。

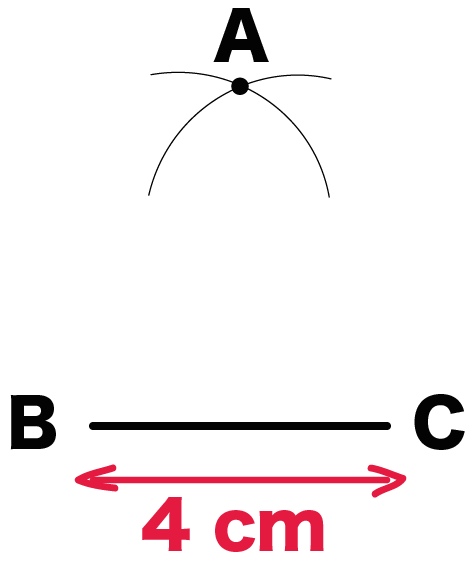
• AとB
• AとC

を定規でむすべばいいんだ。

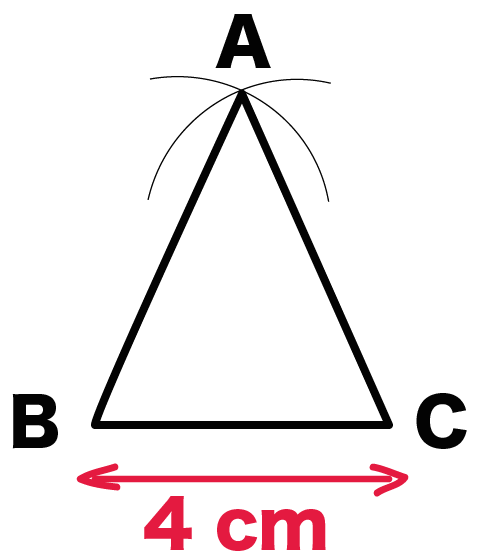
ABとACの長さは6cmになっているはず。

なぜなら、

チョビ円の半径を6cmにしたからね。

おめでとう！

これで二等辺三角形の作図もマスターだね^^

まとめ：二等辺三角形の書き方・作図は辺の長さに注意！

二等辺三角形の書き方はどうだったかな？？

基本的には、

• 三角形の作図・書き方
• 正三角形の作図・書き方

とおなじ！

二等辺三角形の作図では、

「底辺」と「等しい2辺」の長さが違う

ってことに気をつければ大丈夫。

コンパスの脚の長さに注意してね^-^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。