【中学数学】たすき掛け因数分解のやり方がわかる5つのステップ

たすき掛けの因数分解のやり方がわからない？？

こんにちは！この記事をかいているKenだよ。紅茶は午後にかぎるね。

因数分解にはいろいろな問題があるよね。

ときどき、ぜんぜん解けなくて泣きたくなるときも、ある。

よくあるのが、

因数分解の公式が使えない

とか、

共通因数でくくれない

って問題だと思うんだ。

そんなときに助けてくれるのが、

たすき掛けの因数分解

だ。

たすき（襷）といえば、

駅伝とか、

宴会の余興をイメージしちゃうかもね。

だけど、因数分解にもじつは、

たすき掛けという解き方があるんだ。

今日は、この解き方を5ステップで解説していくよ。

よかったら参考にしてみてね。

たすき掛けの因数分解のやり方がわかる5つのステップ

さっきもいったけど、

たすき掛けはつぎのときに役立つよ。

• 因数分解の公式が使えないとき
• 共通因数でくくれないとき

たとえば、つぎの例題みたいにね。

なぜなら、

公式は使えなさそうだし、

共通の因数もぜんぜんみつからないからね。

まさに、たすき掛けの因数分解にはもってこいの問題だ。

今日はこの例題をいっしょにといてみよう！

Step1. 線をかく

まずは、まっすぐな線をかいてみて。

定規は使わなくて大丈夫。

フリーハンドでいいから、すーっと直線をかいてみてね。

これが第1ステップ！

Step2. 係数をならべる

つぎは、直線の下に係数をならべよう。

かりに、

ax² + bx +c

を因数分解するなら、

a、c、b

の順番に係数をならべてあげるんだ。

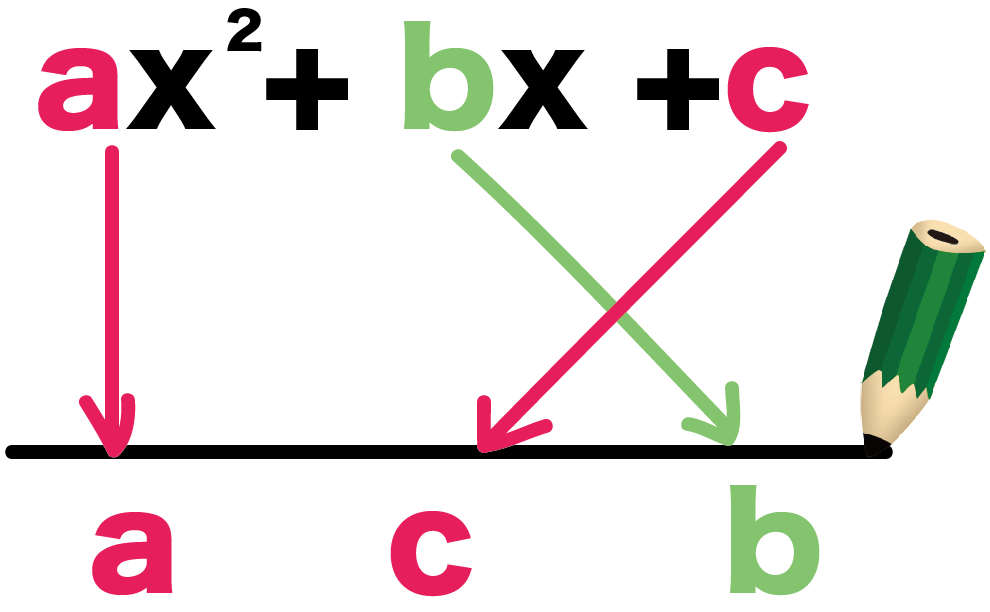
つまり、

1. xの二乗の係数
2. 定数
3. xの係数

ってかんじで左から順番にね。

例題の、

3x² + 5x -2

でもおなじさ。

直線の下に、左から、

• 3
• -2
• 5

の順番に係数をかけばいいんだ。

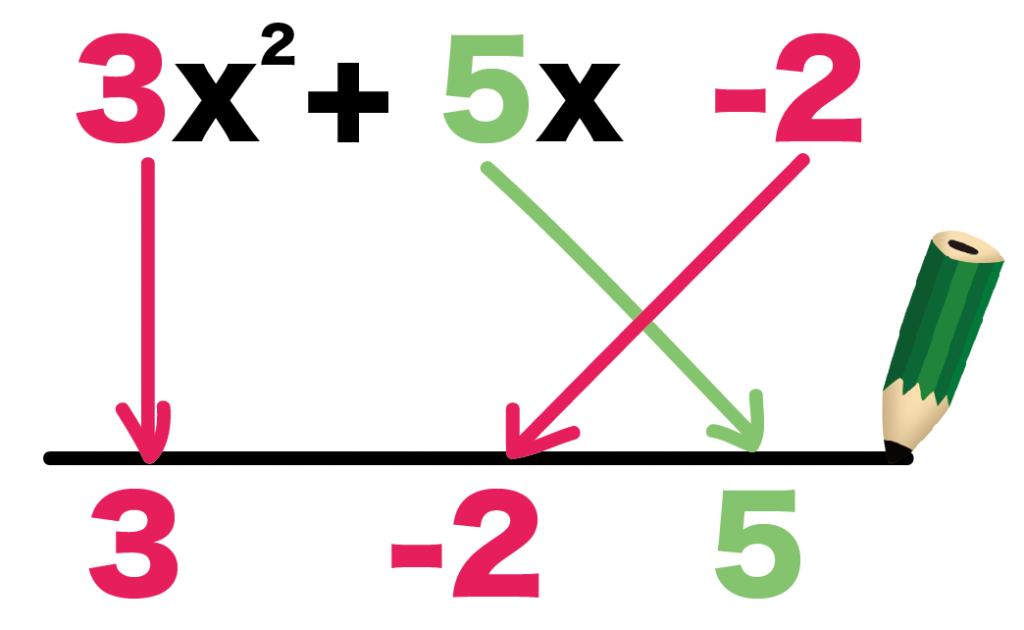
真ん中のxの係数がトリッキーな動きをするから、

順番を間違えないようにね^^

Step3. かけ算のパターンを考える！

つぎは、かけ算のパターンを考えてみよう。

左2つの係数の、

• x2乗の係数
• 定数の係数

になる組み合わせをみつければいいんだ。

たとえば、

ax² + bx +c

だったら、

• かけたらaになる2つの数字
• かけたらcになる2つの数字

をさがせばいいんだよ。

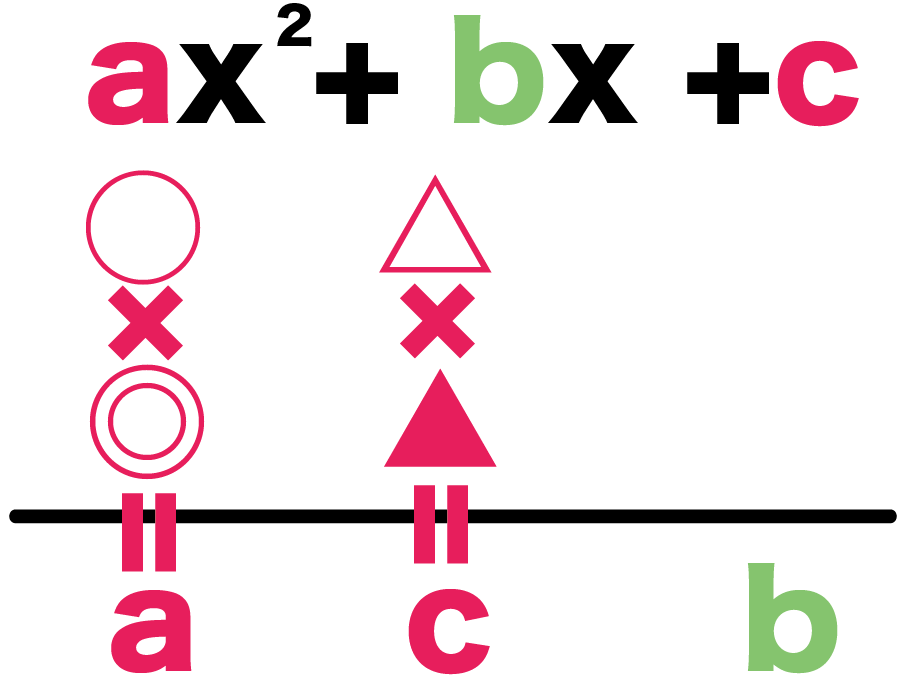
例題でいうと、

• かけて3
• かけて-2

の組み合わせだね。

かけて3になるのは、

• 1×3
• -1×(-3)

の2つかな。

かけて-2になるのは、

• -1×2
• 1×(-2)

の2パターンだね。

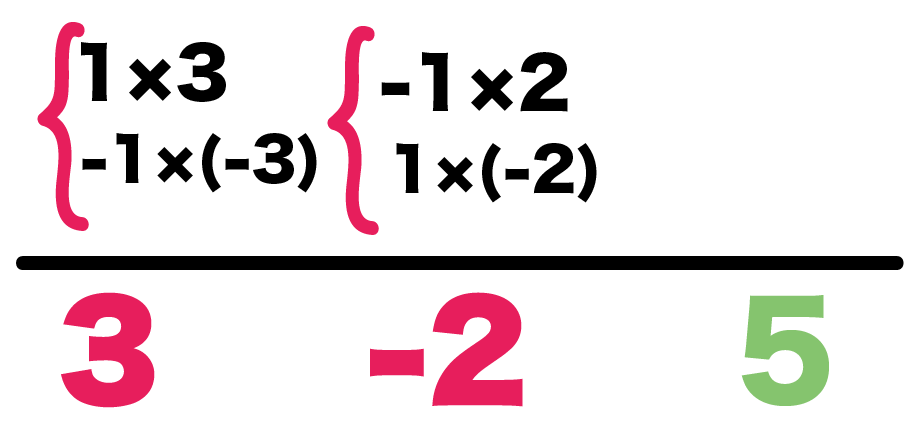
これで第2ステップ終了！

Step4. たすき掛けになる組み合わせをえらぶ

さっきの数字の組み合わせの中から、

たすき掛けの計算にはまるもの

をえらぼう！

えっ。たすき掛けの計算とか知らないって？？

たすき掛けの計算とはずばり、

斜めの数字同士をかけたやつらをたすと、右下の数になる

ってやつなんだ。

たとえば、

ax² + bx +c

だったら、

• ○×◎=a
• △×▲=c
• (○×▲)+(◎×△)=b

になるような、○・◎・△・▲の組み合わせをみつければいいんだ。

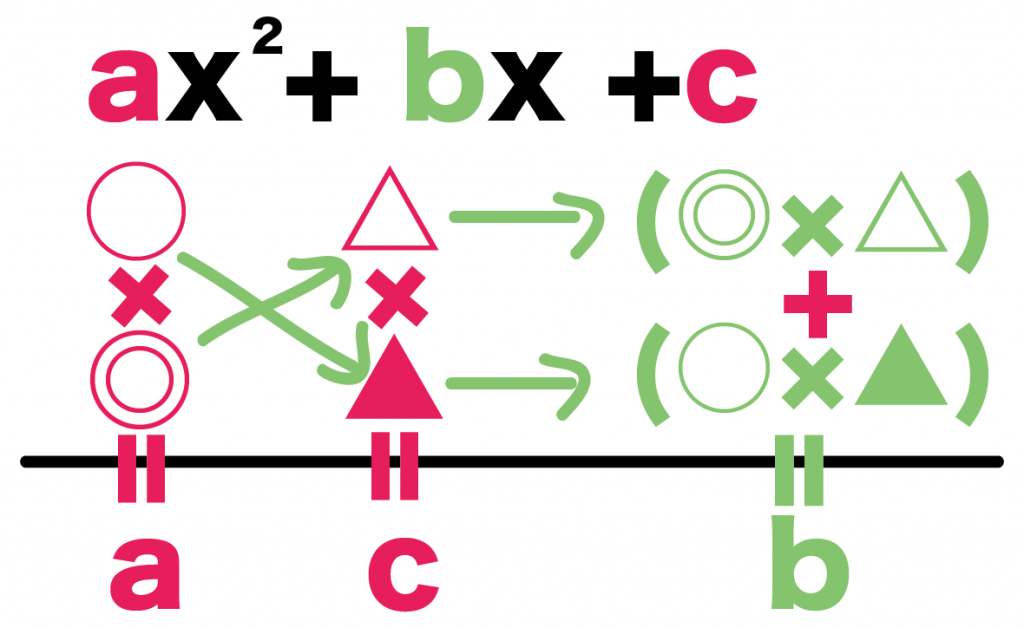
言葉では説明しずらいから例題をみてみよう。

これは力技だ。

当てはまりそうな数をいれて、たすき掛けを試してみよう。

かけたら3になる組み合わせとして、

• 3
• 1

の2つをぶちこんでみる。

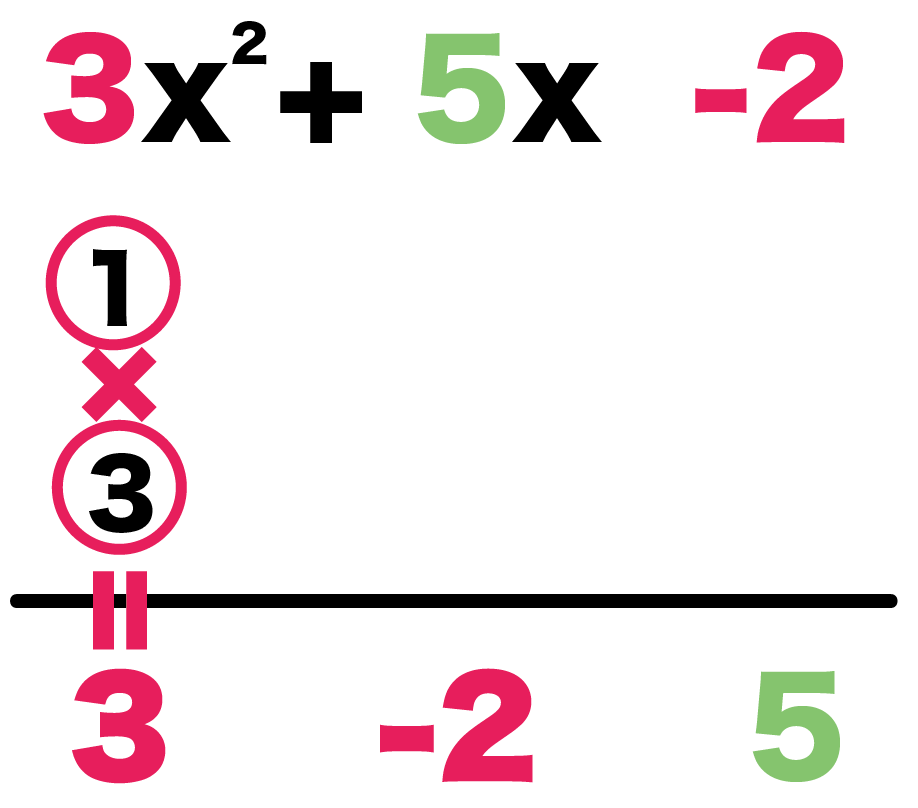
つぎはかけたら-2になる組み合わせだ。

• -2
• 1

のペアーなんてどうだろう？？

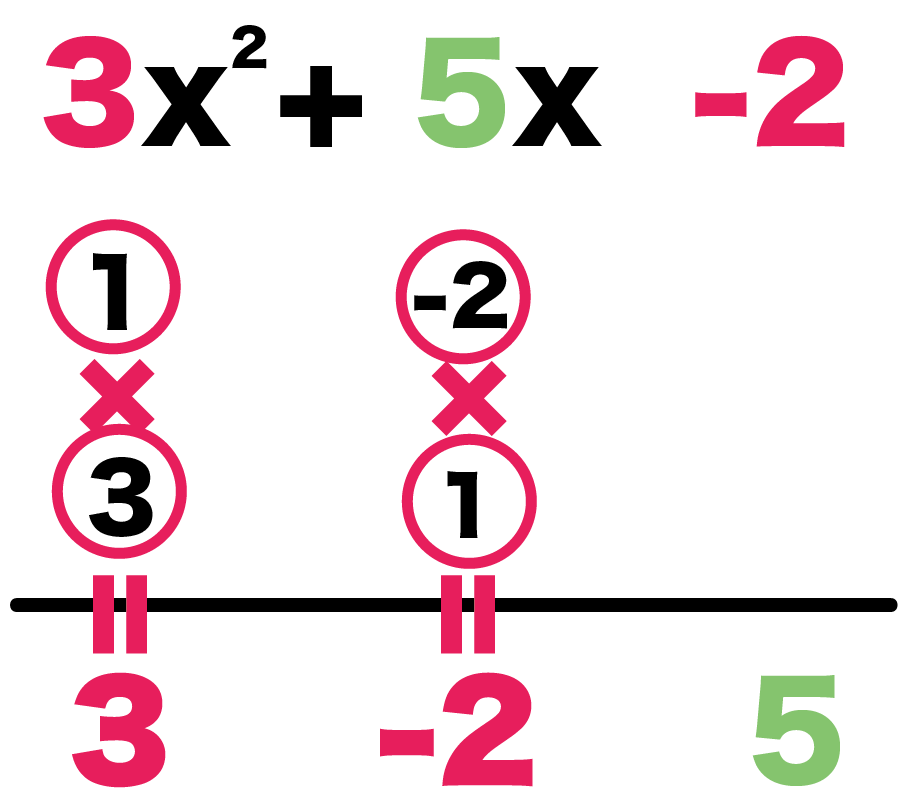
この4つの数字でたすき掛けしてみると、

• 3×(-2) = -6
• 1×1 = 1

になる。こいつらをたすと、

-6 + 1 = -5

になるね。

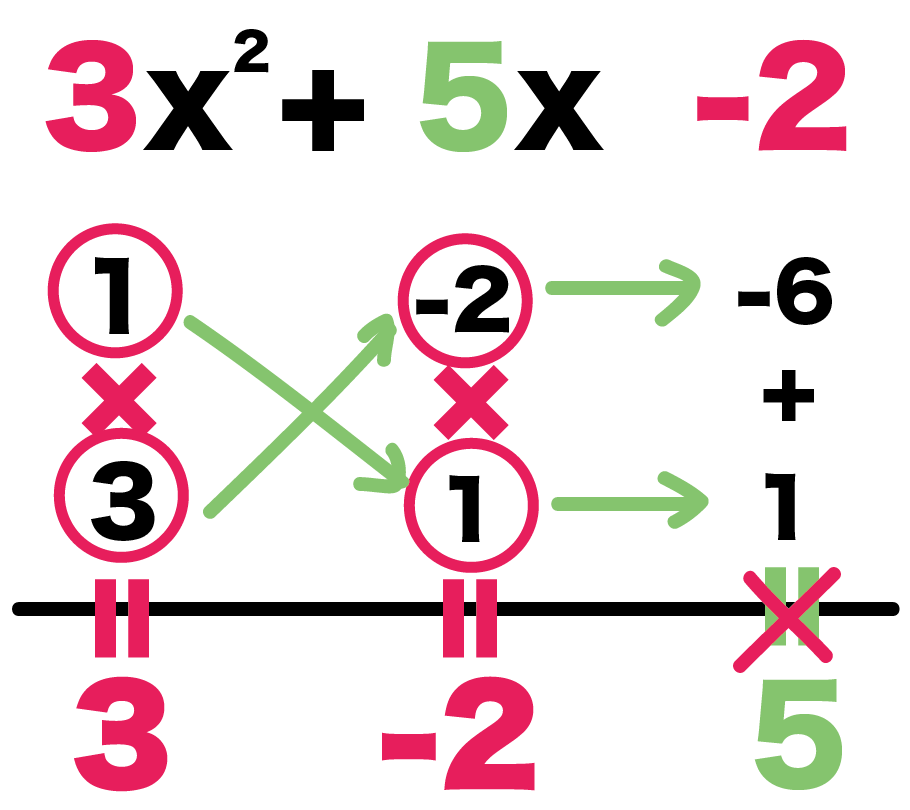
こ、こいつはxの係数の5じゃない！

この組み合わせじゃダメだ！！

じゃあさ、

-2と1の符号を入れ替えたらどうよ？？

-1 と2って感じでさ。

そうすると・・・

• 3×2 = 6
• 1×(-1) = -1

になるね。

で、たしてみると、

6 -1 = 5

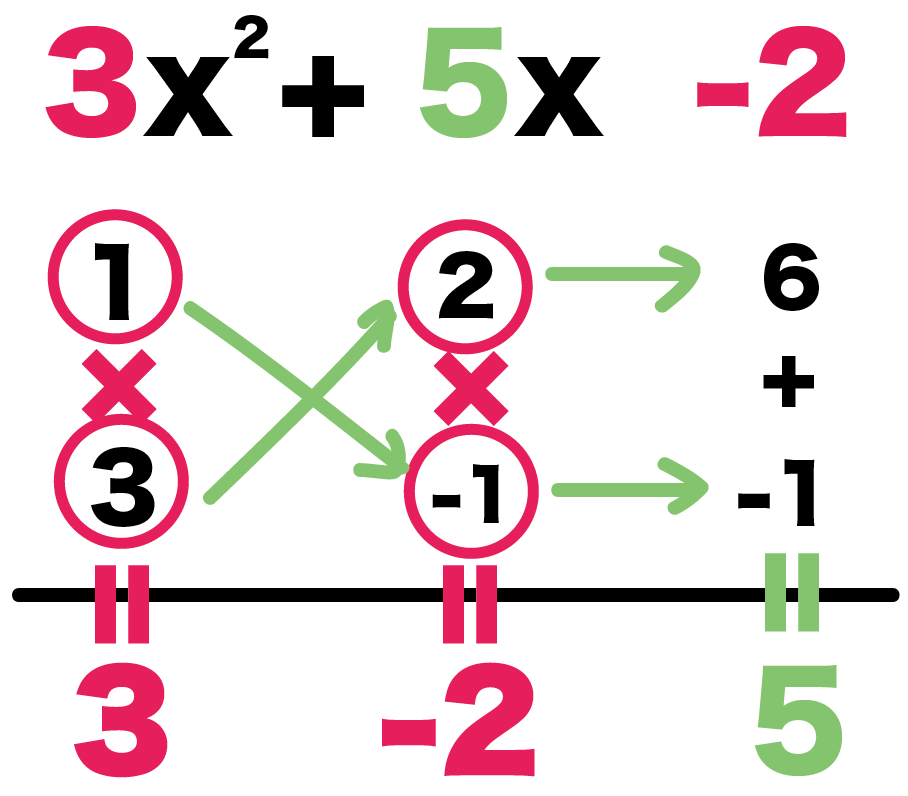
っておおお！

たすき掛け成立しちゃってんじゃん？？

これだ！この組み合わせだ！！

・・・・・・・・

・・・・・・・・

っていうかんじで、

因数を変更してみたり、

符号を変えたりするんだ。

たすき掛けの因数分解になるまでねばってみよう笑

Step5. 因数分解っぽくする

たすき掛けもいよいよ終盤。

たすきがけの組み合わせがわかったら、

因数分解っぽい形にしてみよう笑

たすき掛けで書き出した数字のうち、

いちばん左のやつがxの係数、

真ん中のやつが定数（数字だけの項）になるんだ。

ax² + bx +c

の例だったら、

(○x+△)(◎x+▲)

になるんだ。

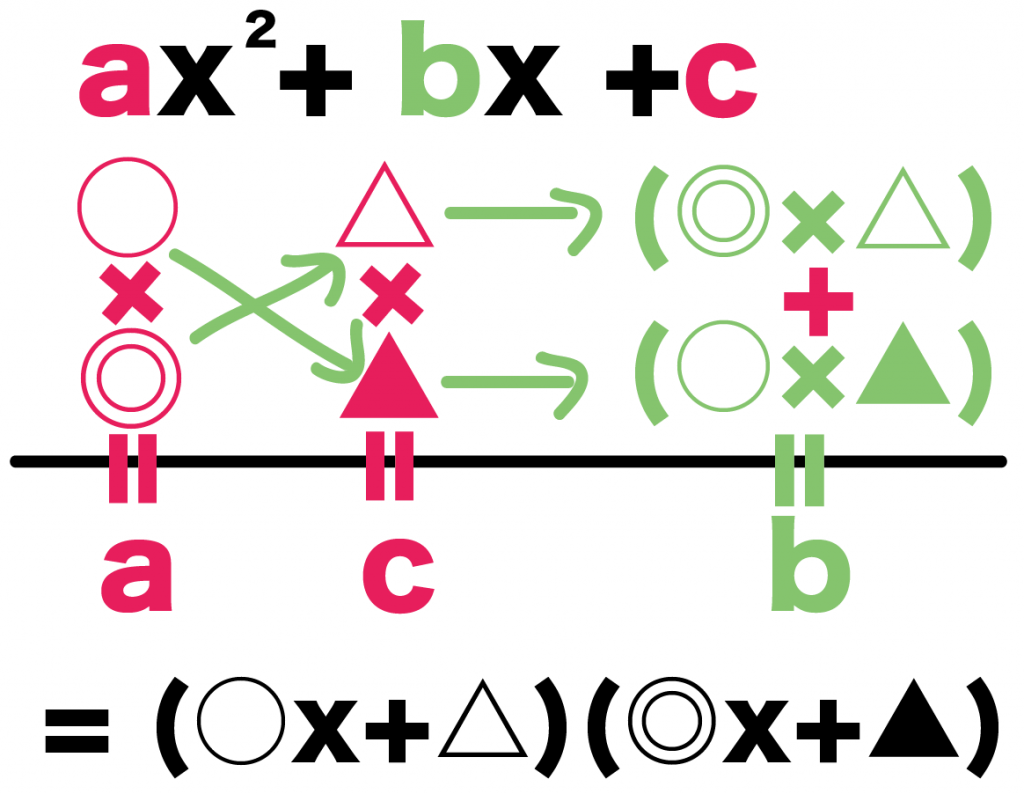
例題では、

• 1と3
• 2と-1

の組み合わせだったね？？

よって、

xの係数は、

• 1
• 3

で、定数の項は、

• 2
• -1

になるんだ。

つまり、

3x² + 5x -2
= (x+2)(3x-1)

になるってわけさ。

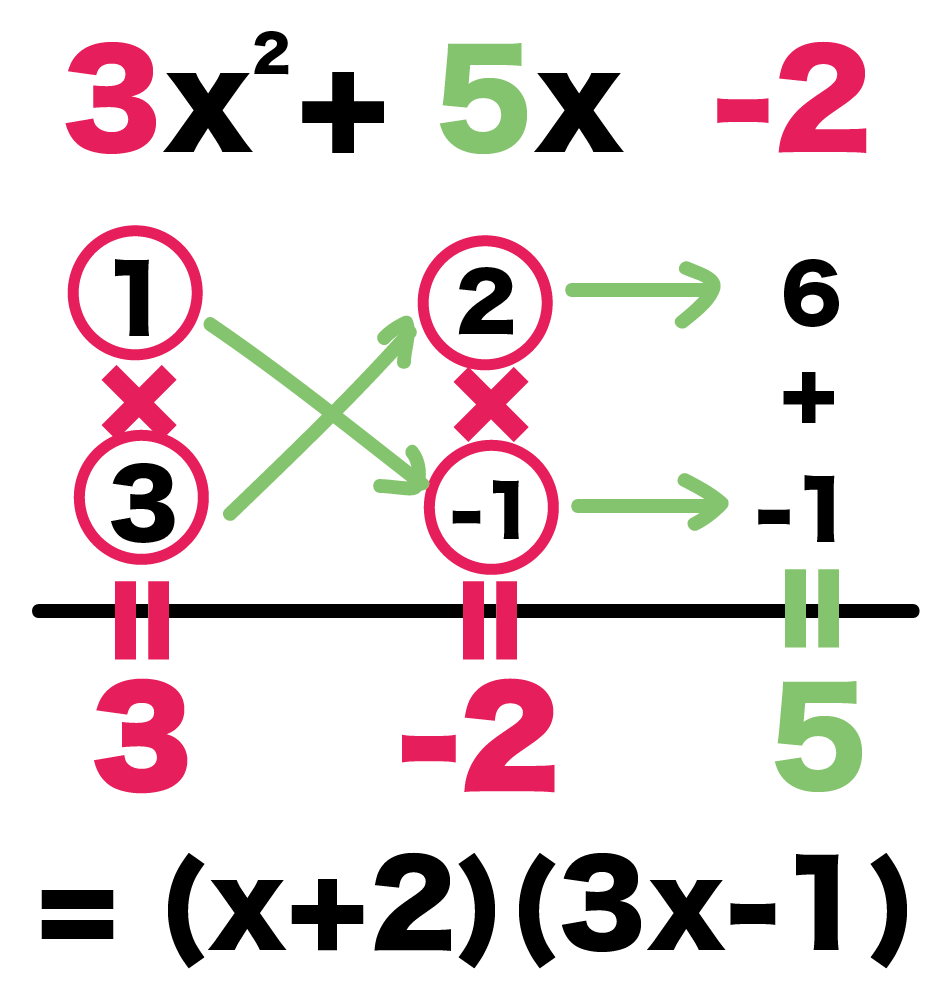
おめでとう！

これでたすき掛けもマスターだね^^

まとめ：たすき掛けの因数分解は気合と根性で乗り切れ！

たすき掛けの因数分解はぶっちゃけむずい。

説明するのも苦しかったよ。うん。

だけど、解き方をおぼえちゃえばもうね、無敵。

必殺ワザをおぼえるものだと思って、

たすき掛けをマスターしちゃおう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。