【中2数学証明】三角形の内角の和の求め方がわかる3ステップ

三角形の内角の和の証明がわからん？？

こんにちは！この記事をかいているKenだよ。天満宮にいきたいね。

三角形の内角の和は「180°」になる

って知ってた？？

つまり、

中の角度をぜんぶ足すと180°になるってことさ。

これはこれで、

うわーすげーー

ってなるよね？笑

ただ、いちばん大切なのが、

なぜ、三角形の内角の和が180°になるのか？？

ってことだ。

これを知っていればクラスでモテるかもしれない。たぶん。

そこで今日は、

三角形の内角の和の求め方の証明

を3ステップで解説していくよ。

よかったら参考にしてみて^^

三角形の内角の和の証明がわかる3ステップ

さっそく証明していこう。

三角形ABCをつかっていくよ。

Step1. 底辺を右にのばす

まずは底辺を右にすーっと伸ばしてみて。

三角形ABCでいうと辺BCだね。

こいつを右にのばして、

伸ばした先を、なんだろうな、Dとでもおこう。

これがはじめの一歩さ。

Step2. 平行線を1本ひく！

つぎに平行線を一本ひくよ。

伸ばした底辺の頂点を通る平行線をひいてみて。

向かい側の辺に平行な直線ね。

三角形ABCでいうと、

Cを通ってABに平行な直線だね。

そうだなあ、平行線の先をEとでもおこうか。

これが第2ステップ。

Step3. 平行線の性質を使う！

最後に平行線の性質をつかっちゃおう。

平行線の性質って、

• 同位角は等しい
• 錯角は等しい

の2つだったよね？？

これを平行線でつかってやればいいんだ。

三角形ABCではABとCEが平行だったね。

錯角は等しいから、

角BAC　＝　角ACE

になる。

また、同位角をつかってやれば、

角ABC ＝　角ECD

になるね。

ここで、

頂点Cに注目してみて。

この頂点には

• a
• b
• c

という3つの角度があつまっているよね。

そんで、3つで1つの直線になっている。

ってことは、

ぜーんぶ足し合わせたら180°になるってことさ。

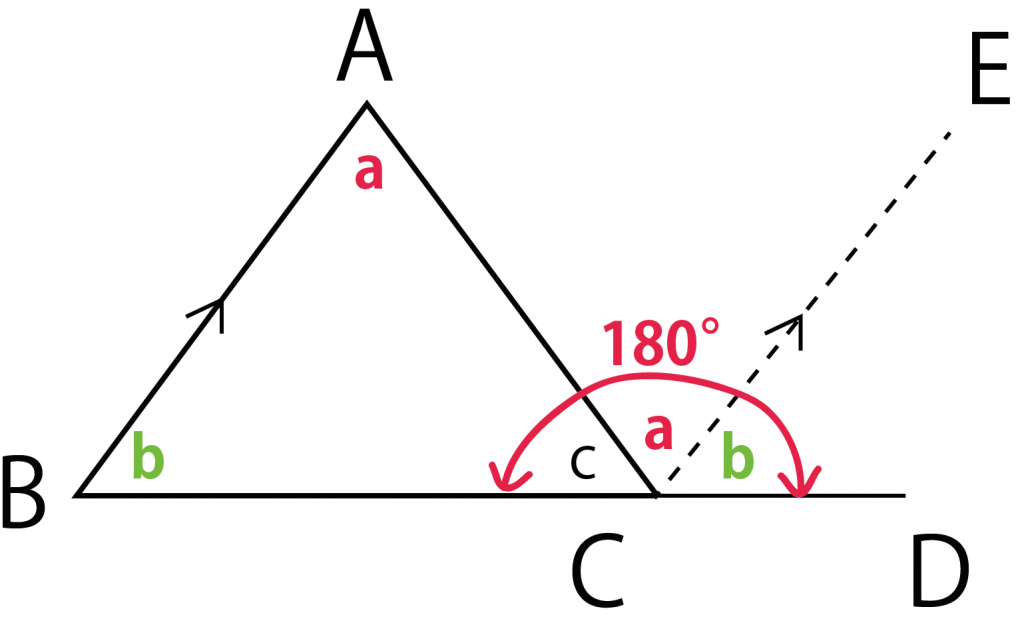
つまり、

a + b + c ＝ 180°

ってことがいえるね。

「a + b + c」は三角形の内角をぜんぶたした和。

だから、

三角形の内角の和は180°になる

ってことが言えるのさ。

まとめ：三角形の内角の証明は平行線をつかえ！

三角形の内角の和の証明は、

平行な補助線をひくことがポイント。

ここさえできればあとはお茶の子さいさいさ。

テストにも出やすいからよく復習しておいてね^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。