正四角錐の表面積の求め方って??
こんにちは、この記事をかいているKenだよ。鶏肉は煮るとウマいね。
正四角錐って、
底面が「正方形」の錐体のこと
だったよね??
つまり、底面が正方形で、先がとんがっている立体ってことだ。
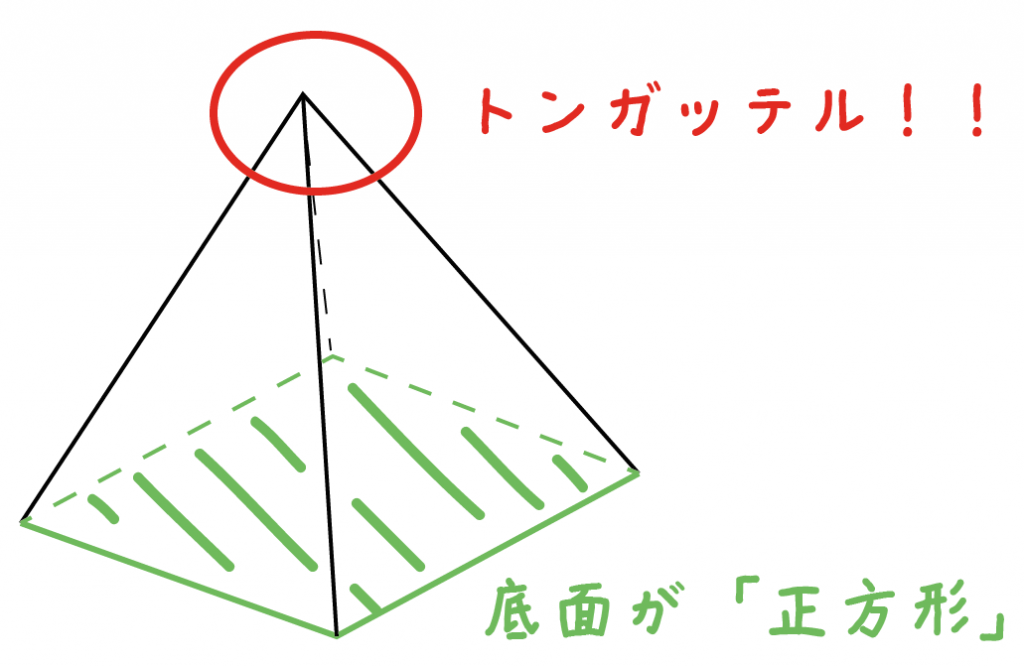
そんな正四角錐の表面積は
(底面の正方形)+(側面の三角形)×4
で求めることができるよ^^
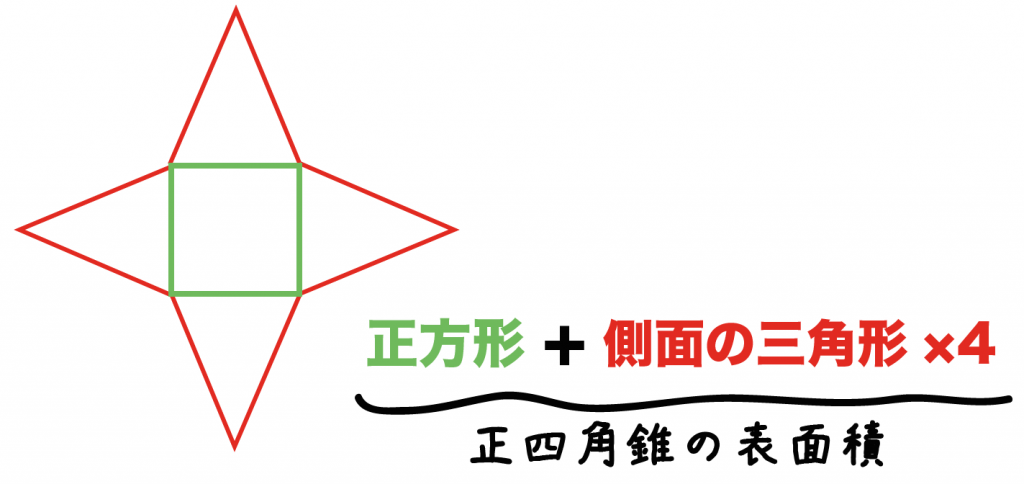
だって、正四角錐の展開図が「正方形1つ」と「三角形4つ」で成り立っているからね^^
つまり、
「底面の1辺の長さ」と「側面の三角形の高さ」がわかっていれば計算できるってわけさ。
えっ。どんな問題がわからないから怖すぎるだって!?
そ、そんなキミでも大丈夫。
じつは、中学数学ででてくる「正四角錐系の問題」ってだいたい次の3つのパターンになるんだ。
- 「正方形の1辺の長さ」と「側面の三角形の高さ」がわかっているパターン
- 「正方形の1辺の長さ」と「正四角錐の他の辺の長さ」がわかっているパターン
- 「正方形の1辺の長さ」と「正四角錐の高さ」がわかっているパターン
それぞれの求め方についてゆっくりみていこう。
「正方形の1辺」と「側面の三角形の高さ」がわかっている問題
いちばん簡単なパターン。中学1年生でもとける問題だね。
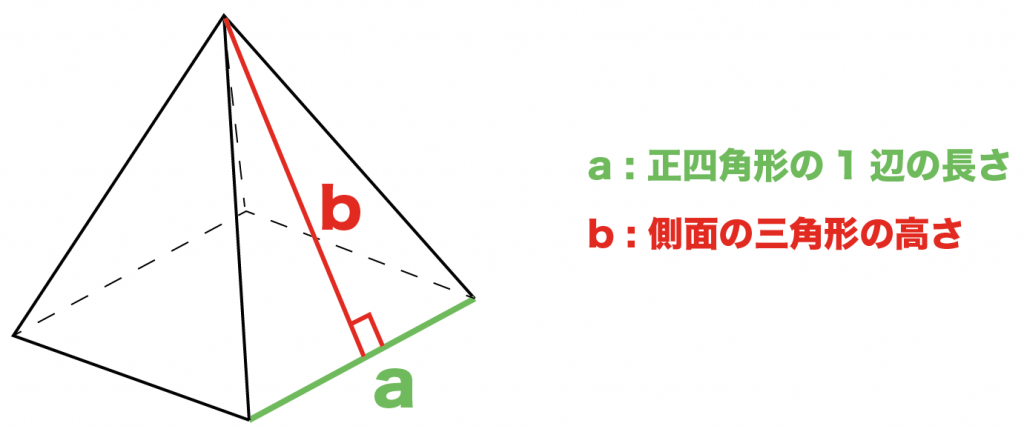
「底面の1辺の長さ」と「側面の三角形の高さ」がわかっているから、
「底面の正方形」+「側面の三角形」×4
を計算すればいいんだ。
たとえば、底面の1辺の長さが4cm、側面の長さが6cmだとしよう。
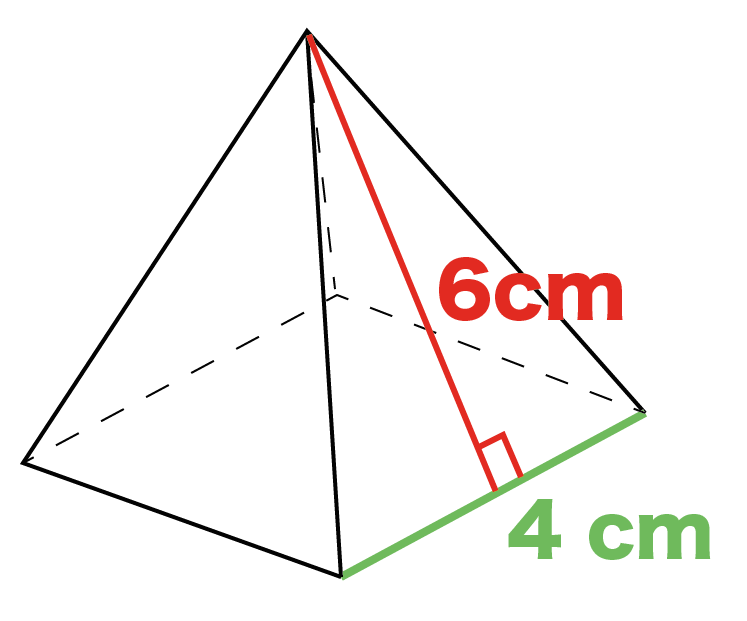 正四角錐の展開図は「底面の正方形1つ」と「側面の三角形4つ」で構成されているね。
正四角錐の展開図は「底面の正方形1つ」と「側面の三角形4つ」で構成されているね。
よって、正四角錐の表面積は、
( 4×4 ) + ( 4×6÷2 ) × 4
= 64 [cm²]
になる。
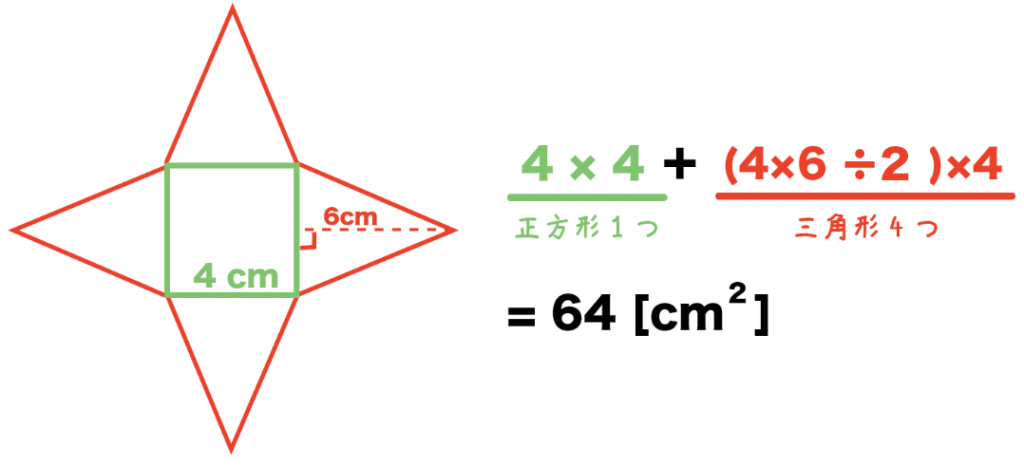
中1数学ではこの種類しか出題されないよ^^
しっかり押さえておこう。
「正方形の1辺」と「側面の三角形の辺の長さ」がわかっているパターン
2つ目のパターンは、
「正方形の1辺」と「側面の三角形の辺の長さ」がわかっているパターンだ。
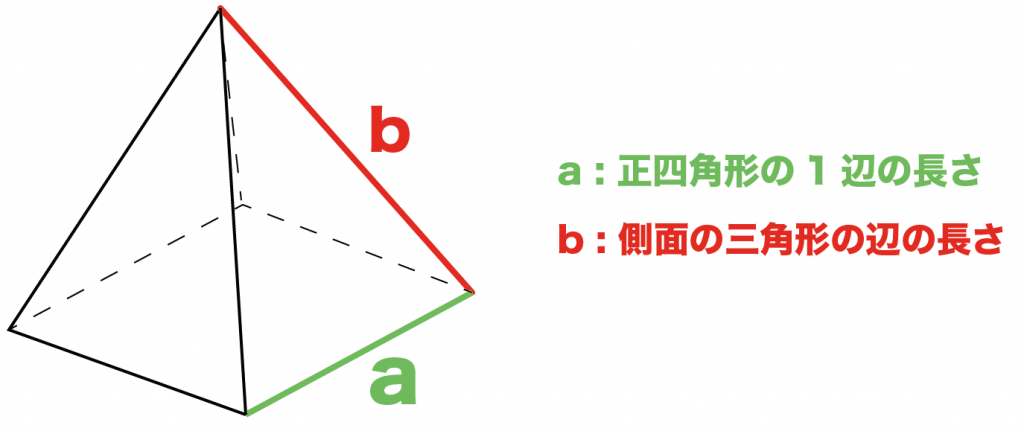
正四角錐の表面積の求め方って、
側面の三角形の高さ
さえわかっていれば計算できちゃう。
ってことは、「正方形の辺の長さ」と「側面の三角形の辺の長さ」から「側面の三角形の高さ」を計算しちゃえばいいってことになるね。
たとえば、
底面の1辺の長さが「6cm」、側面の三角形の辺の長さが「5cm」の正四角錐があったとしよう。

側面の三角形は二等辺三角形だから、頂点から底辺にひいた垂線は垂直二等分線になっているね。
側面の三角形の高さhは、三平方の定理をつかうと次のように計算できる。
√(5² – 3²)
= 4
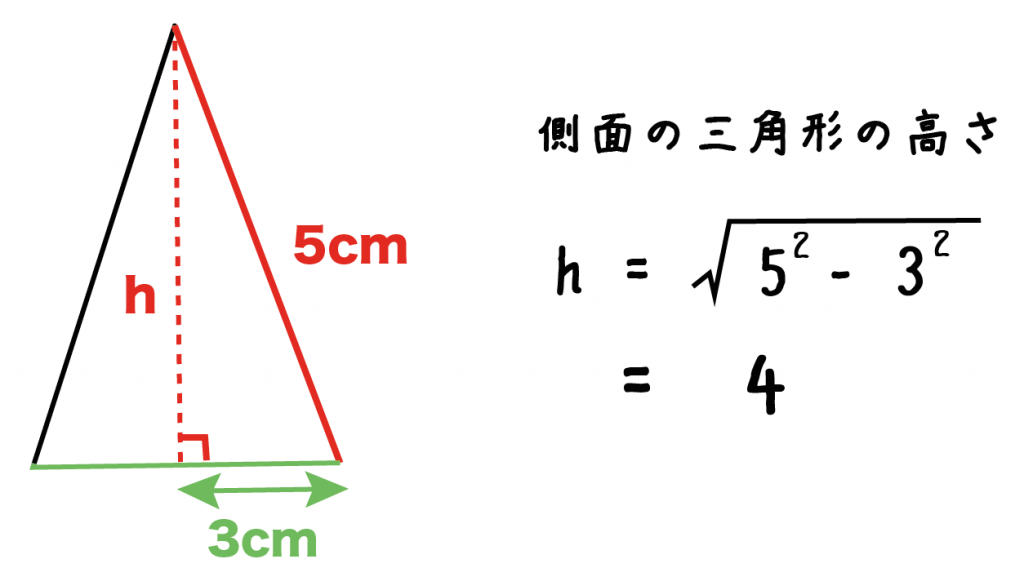
側面の三角形の高さがわかったらもう大丈夫。
正四角錐の表面積は、
「底面の正方形」+「側面の三角形」×4
だったよね?? これも1つめのパターンと同じように計算してやると、
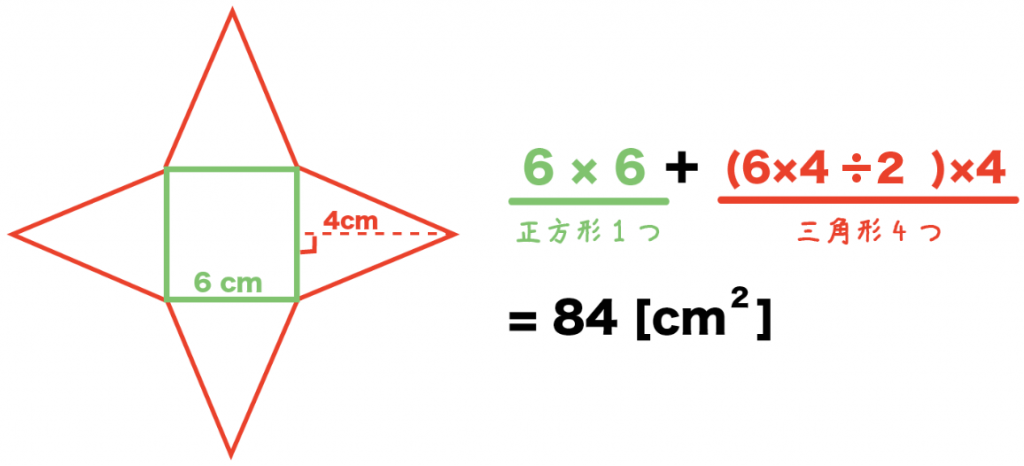
6×6 + (6×4÷2) ×4
= 84[cm²]
っていう感じで、正四角錐の表面積が計算できちゃうんだ。やったね^^
「正方形の1辺」と「正四角錐の高さ」がわかっているパターン
最後は「正方形の1辺の長さ」と「正四角錐の高さ」がわかっているパターンだよ。
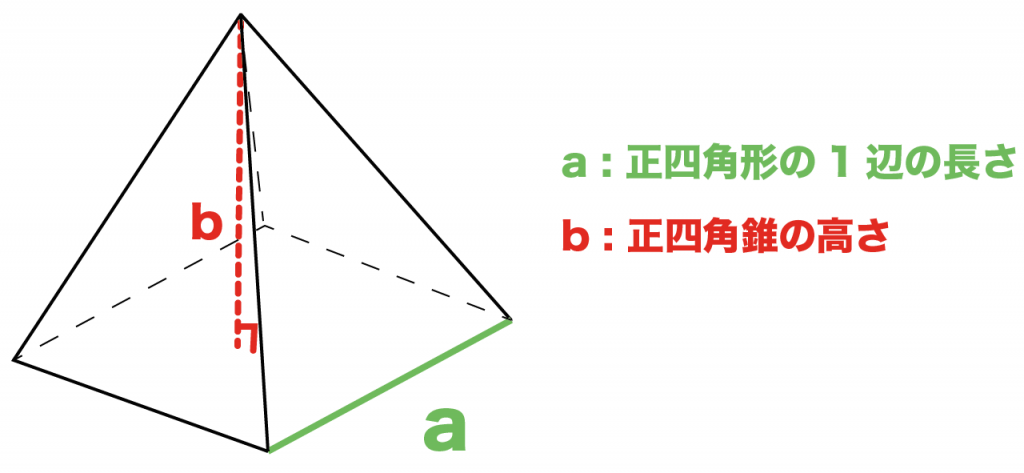
これもさっきのパターンと同じで、
「正方形の1辺の長さ」と「正四角錐の高さ」から「側面の三角形の高さ」をだしてやれば表面積を求めることができるよ^^
たとえば、
底面の1辺の長さが「8cm」、高さも「8 cm」の正四角錐があったとしよう。
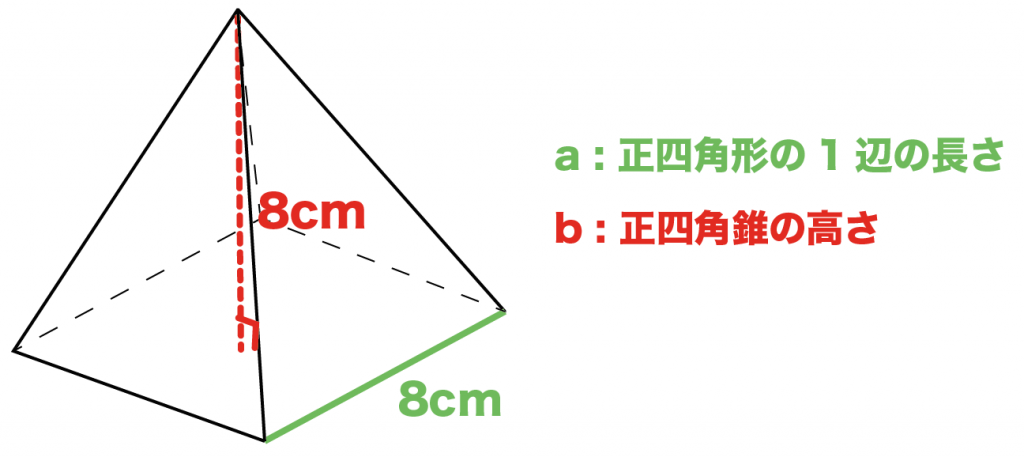
このとき、
「正四角錐の高さ」と「側面の三角形の高さ」を1辺とする三角形を考えてみよう。
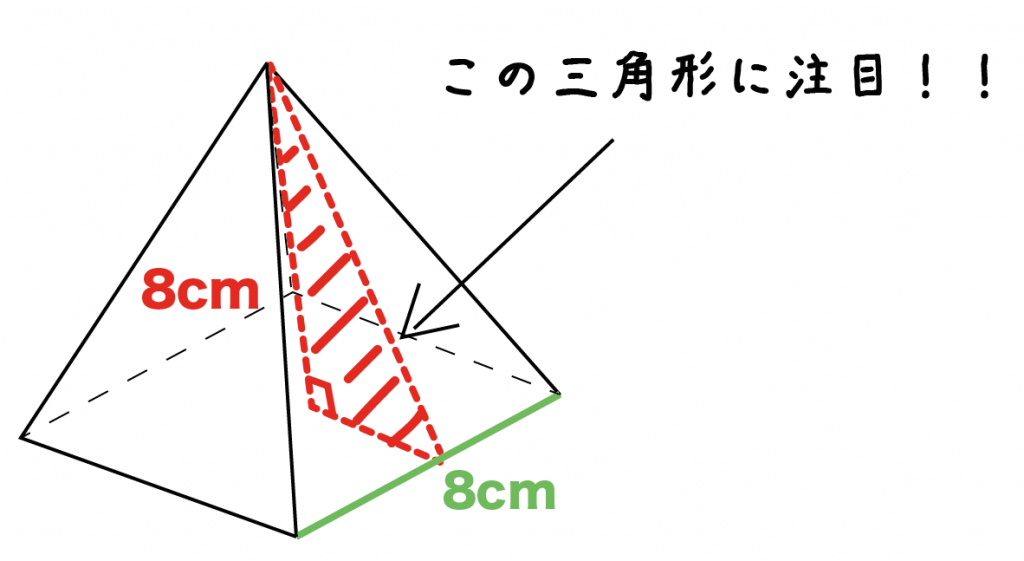
正四角錐の頂点からおろした垂線は、ちょうど底面のど真ん中に着地しているね。
だから、この三角形の底面は正方形の辺の半分の「4cm」になる。
三平方の定理をつかって、斜面の長さを求めてやると、
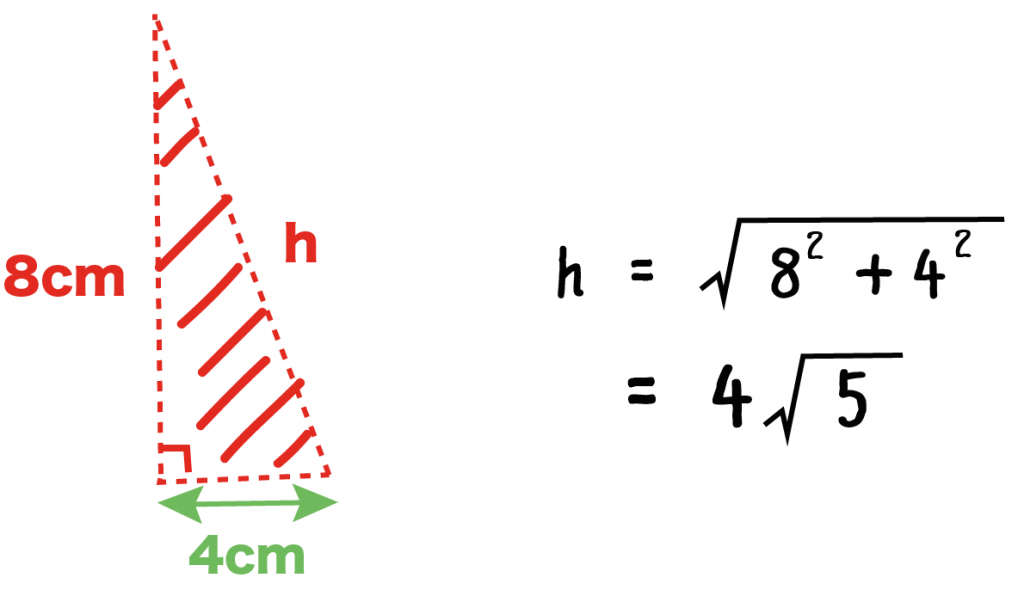
h = √(8² + 4²)
= 4√5
になる!
側面の三角形の長さがわかってしまえばあとは計算するだけ。
正四角錐の表面積は、
「底面の正方形」+「側面の三角形」×4
で求めることができるから、
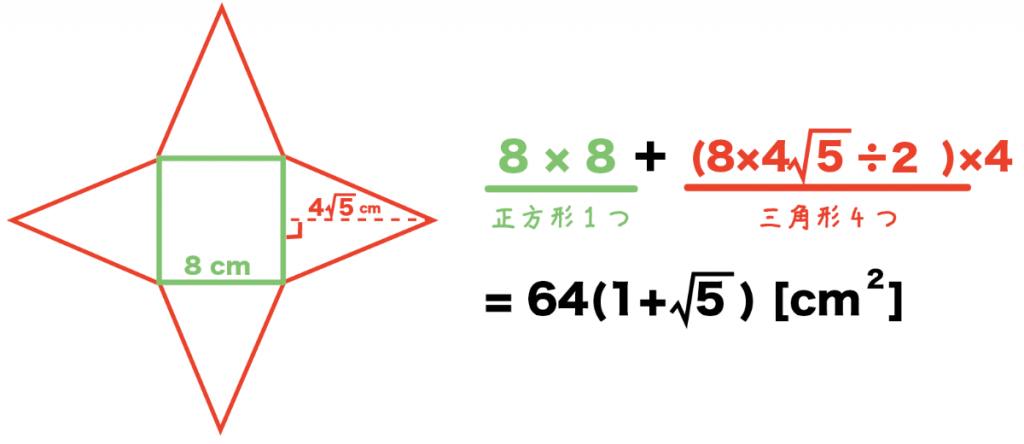
( 8 × 8 ) + (8×4√5 ÷2 ) × 4
= 64 ( 1 + √5) [cm²]
となる。
おめでとう!これで正四角錐の表面積が計算できたね^_^
まとめ:正四角錐の表面積の問題は3通り
正四角錐の表面積の求め方の問題がでたら、
自分が解こうとしている問題がどのタイプか??
ということを探ってみよう。そして、
いかにして側面の三角形の高さをだすか??
ということを考えてみよう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。





四角錐の体積を教えて
正四角錐の体積の求め方を読んでみて
円錐の表面積を教えてください。
>円錐の表面積を教えてください。
円錐の表面積の求め方を読んでみて
座標から式を考える
>1.5<√m<3
不等式の端っこと端っこを二乗してmの範囲を求めてみようぜ
正四角錐の展開図の三角形の角度を教えてください。
>正四角錐の展開図の三角形の角度
正四角錐ごとによるかな!
0.5ってなんだー!
>0.5ってなんだー!
三角形の面積の公式だね!
2分の1が0.5になってるよ!
正四角錐の計算を小4でもわかりやすく教えてください
0.5じゃなくて÷2でもいいのですか?
>0.5じゃなくて÷2でもいいのですか?
いいよ!x0.5と÷2は同じだ!
急いでます!
簡単に公式が覚えられる方法などありますか?
>急いでます!
簡単に公式が覚えられる方法などありますか?
数学の公式は使って覚えるのが一番!
すごく分かりやすかったです!
ありがとうございました♥
円錐の体積の求め方を教えてください!
円錐の体積の求め方を読んでみて!
正四角錐の高さがわかっているときと、三角形の辺の長さがわかっていて、どちらの長さが違うときはどうやって求めればいいですか?
どうにかして底面積がわかれば体積を計算できるね。
おそらく側面の三角形の情報から三平方の定理を使って底面の辺の長さを出すのかな
どっから0.5が出てきたのかわかりません。
これは÷2と同じだ!確かに分かりづらいから修正しておこう
分かりやすかったです
ありがとうございました
本当に分かりやすい公式を教えてくださりありがとうございます
超分かりやすかったです
ありがとうございました
馬鹿だけど計算できました
ありがとうございます
公式の底面の正方形+側面の三角形×4の×4って、足し算の式が終わった(?)後ですか?それとも()がないから普通でいいんですか?