球の体積と表面積の公式をごちゃまぜにしない2つのポイント

球の体積と表面積の公式がごっちゃごちゃ！

こんにちは！この記事をかいているKenだよ。アップルティーはいつ飲んでもうまいね。

中学数学ででてくる球の公式って次の2つあったよね？？

• 球の体積の求め方：「4/3πr³」
• 球の表面積の求め方：「4πr²」

※球の半径をrとした場合

この2つの公式を覚えていないとテストで問題をとけないし、

クラスの人気ものにはなれない。

しかも、がんばって2つとも暗記したとしても・・・・

球の体積と表面積の公式がごっちゃまぜになっちまうかもしれないんだ。

たとえば、

4πrの二乗って数式は覚えてるんだけど・・

これって・・・体積・表面積のどっちだっけ？？

みたいな感じでね笑

今日はそんな緊急事態を避けるため、

球の体積と表面積の公式を見分けるポイント

を2つ紹介するよ。

テスト本番で公式を忘れるのが怖いっていうときに参考にしてみて^^

球の体積と表面積の公式を見分ける2つのポイント

球の体積と表面積の公式をごっちゃまぜにしないためポイントはつぎの2つさ。

ポイント1.  「rの乗数」をみる！

1つ目のポイントは、

rが何乗されているか？？

ということを確認する方法だ。

つまり、rの乗数をチラ見するってわけ！

rが何乗されているかによって、

次のように「体積」と「表面積」の公式を見分けることができるよ。

• rが二乗されている公式→「球の表面積」
• rが三乗されている公式→「球の体積」

つまり、

4/3πrの三乗という公式は「rが三乗されている」から「球の体積の公式」ってこと！

また、

4πrの二乗は「rが二乗されている」から「球の表面積の公式」になるってことだね。

二次元の表面積を計算するときは「rを2回かける」、

三次元の立体の体積を計算するときは「rを3回かける」、

って感じでrをかける回数をおぼえておこう！

球の体積と表面積の公式がごちゃまぜになったときは、

rが何乗されているのか？？

ということを必ず確認してみてね^_^

ポイント2. 「1/3」をかけるのは体積の公式！

2つめのポイントは、

1/3をかけているかどうか

だ。

もし、1/3が混じっている公式ならそいつは「球の体積の公式」ってことになるよ。

とくに理由はないんだけど、

1/3をかけるのは「錐体（先がとんがっている立体）」の体積の公式と同じでしょ？？

たとえば、四角錐の体積の求め方とかね。

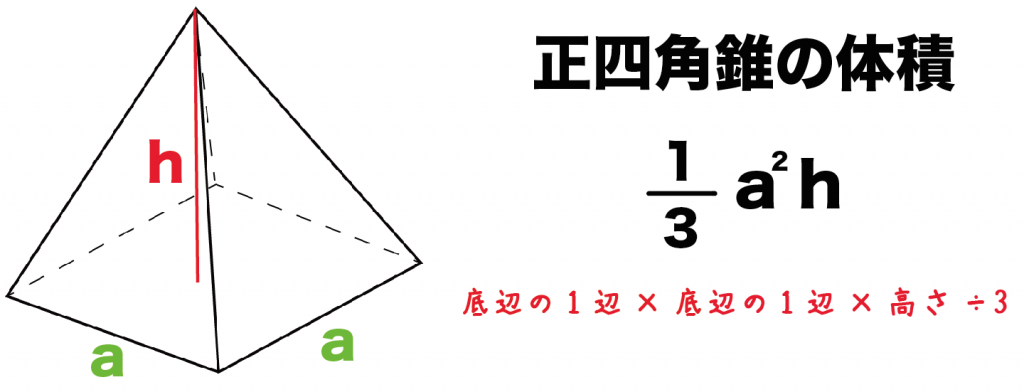
だから、錐体の体積の求め方と同じように「1/3」をかけている計算式は「球の体積の公式」だよ

っておぼえておこう！！

これなら表面積の公式とごっちゃにならないはず^^

まとめ：球の体積と表面積の公式はごっちゃにならんぜ！

上の2つのポイントを覚えておけば、

球の体積と表面積の公式をごちゃまぜにする

というミスはないはずだ！

本番前にはもう一度公式を確認してみてねー！

そんじゃねー

Ken
なぜ球の体積の公式がつかえるか気になったらみてみて↓

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。