二次方程式の利用の文章問題の解き方??
こんにちは!この記事をかいているKenだよ。山の日は混むね。
二次方程式の解き方をたくさん勉強してきた。
因数分解をつかった解き方とか、
解の公式でとくやり方とかね。
ぶっちゃけ、
どんな二次方程式もとける自信あるよね??
だがしかし、中3数学の二次方程式はまだこれからなんだ。
二次方程式のゴールは、
二次方程式を文章問題でも使えるようになる
なんだよね。
そこで今日は、
二次方程式の利用の文章題の解き方
をわかりやすく解説してみたよ。
よかったら参考にしてみてね。
二次方程式の利用の文章題の解き方がわかる4ステップ
二次方程式の利用の解き方を解説していくよ。
つぎの練習問題をといてみよう。
練習問題
2つの連続する正の偶数の積が168になるとき、2つの偶数をそれぞれ求めなさい。

どんな文章題でも、4ステップでとけちゃうんだ。
- 求めたいものを文字とおく
- 二次方程式をたてる
- 二次方程式を解く
- 解を吟味する
Step1. 求めたいものを文字とおく
文章問題で求めたいものを文字でおこう。
辺の長さを求めたいときは「辺の長さ」、
ケーキの値段をだしたいときは「ケーキの値段」を文字でおけばいいのよ。
練習問題では、
積が168になる「2つの連続する正の偶数」
を求めたかったよね??
だから、「2つの連続する偶数を文字」であらわせばいいのさ。

正の整数nで連続する偶数をあらわしてみよう。
※numberのnからきてるのさ。
ある偶数は、正の整数を2倍するとなるから、
2n
になるよね??
そのつぎの偶数はこいつより2大きいはずだから、
2n + 2
になるはず。
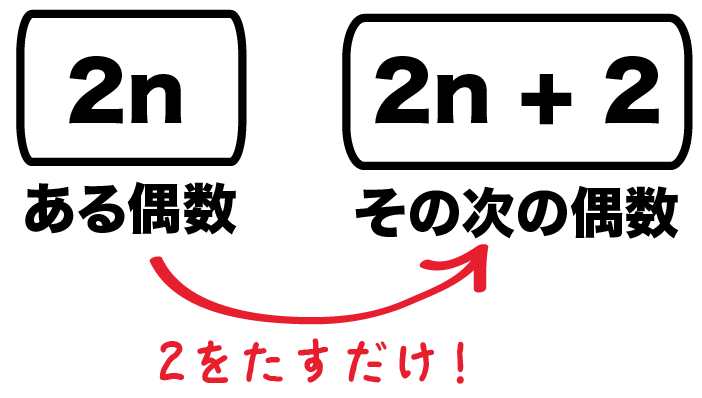
これが第1ステップだ。
Step2. 二次方程式をつくる
つぎは二次方程式をつくってみよう。
AがBになるとき
っていう文章をみつけて、「A=B」っていう方程式をたてればいいのさ。

例題では、
2つの連続する正の偶数の積が168になるとき
っていう文章に注目してみて。
ようは、
(2つの連続する正の偶数の積)= 168
っていう方程式をつくればいいんだね。
連続する2つの偶数はそれぞれ、
- 2n
- 2n+2
だったよね??
だから、2つの連続する偶数の積は、
2n (2n + 2)
になる。
こいつが「168」に等しくなるから、
2n (2n + 2) = 168
っていう方程式ができるね。

Step3. 二次方程式を解く
二次方程式を解いてみよう。
2次方程式の解き方はどれをつかってもいいよ。
因数分解でもいいし、解の公式をつかってもいい。
答えがでちゃえば問題ないわけだ。
練習問題の二次方程式は、
2n (2n + 2) = 168
だったよね??

左辺の()を分配法則ではずすと、
2n (2n + 2) = 168
4n^2 + 4n = 168
になる。

んで、移項して両辺を4でわってやると、
4n^2 + 4n – 168 = 0
n^2 + n – 42 = 0
になるね。

左辺の、
n^2 + n – 42
を因数分解してみると、
n^2 + n – 42
=(n +7)(n-6)
になるね。
よって、この二次方程式の解は、
n = 6, -7
だ。

Step4. 解を吟味する
二次方程式は無事とけたかな??
よかった!やったね!!
・・・・・・・・
・・・・・・・・
っていいたいところだけどね。
二次方程式の文章題の本番はこれからなんだ。
なぜなら、
その解が正しいか判断しなきゃいけないからね。
このことを数学界では、
解を吟味する
っていうんだ。
文字の条件を振り返ってみてね。
練習問題では、
- n = 6
- n = -7
がでてきたよね??

ここで、nは何かって振り返ってみると、
正の整数
だったよね??
えっと、、2つとも正の整数かなああ・・・
!!!?
あっ!
正の整数じゃないやつもいるやんけ!
そう。
n = -7
が条件にフィットしてないんだ。負の数だからね。
だから、この「n = -7」は適切じゃないってことがわかる。

したがって、2次方程式の解として正しいのは、
n = 6
だけだね。
よって、n = 6のとき、2つの連続する偶数は、
- 2n = 12
- 2n + 2 = 14
になる!

つまり、積が168になる連続する2つの正の偶数は、
- 12
- 14
の2つになるってわけ。
おめでとう!
これで二次方程式の文章題もマスターだね^^
まとめ:二次方程式の利用の文章問題は解の吟味が大事
二次方程式の文章題はちょっとくせもの。
最後の最後に、
その解が問題として正しいのか??
を確かめなきゃいけないんだ。
最後まで気を引き締めていこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







>連続する2つの正の奇数がある。小さい数の平方と大きい数の平方の和は、2つの数の積に39を足した数に等しくなるという。
この2つの正の奇数を求めなさい。
という問題で、
模範解答では、連続する2つの正の奇数が
x、x+2となっていました。
私は中1の時連続する2つの奇数は2n+1、2n+3などという風に習ったのですが、
現在中2になって、体系問題集の完成ノートにはこのような感じで書かれていました。
どちらが正しいのでしょうか?
2n+1、2n+3の方がいいよ。
なぜなら、x、x+2の場合、xが偶数の時には両方とも偶数になっちまうからね。
文字をある整数で置くなら、まず2倍してあげて、偶数であることを確定して、奇数を足すのが一番
小学6年です。
いつも参考にしております。
お忙しい所すみません><
qikeru様では、応用問題は扱っていないのでしょうか?それとも、このような問題が応用なのですか?
回答お待ちしております。
基本問題を主に取り扱ってるよ!
応用問題はキリがないからね
いつも参考にしております。
【体育館の長いすに全校生徒が座るとき,1脚の長いすに 3人ずつ座ると座席は 8 人分足りず,1脚の長いすに 4 人ずつ座ると座席は 60 人分余る.このとき,長いすの脚数を求めなさい.】
この問題で、3x-8=4x+60と、座れる人数に観点を置いて式を立てたんですけど、x=-68となってしまいます。座れる人数に観点を置いてはいけないのですか?
ちなみに、長いすの脚数をxとおきました。
方程式の問題です!
300円のカゴに1個100円の桃と1個80円のリンゴを合わせて15個つめて、合計1700円になるようにしたい。リンゴは何個つめばよいか。という問題が分かりません!教えてく高い!
>【体育館の長いすに全校生徒が座るとき,1脚の長いすに 3人ずつ座ると座席は 8 人分足りず,
1脚の長いすに 4 人ずつ座ると座席は 60 人分余る.このとき,長いすの脚数を求めなさい.】
>3x-8=4x+60
符号が逆だね。
この等式は「全校生徒の数」が等しいことを等式にしてやればいいから、
足りないときは、長椅子に座った人数+足りない人数で全校生徒数。
逆に、余るときは、その長椅子に座れる椅子の数から余る椅子の数を引けばいいのね
ってことで、
3x+8=4x-60
が正解だ。
なるほど。適当に等式をつくってはいけないのですね。
ありがとうございました。
>300円のカゴに1個100円の桃と1個80円のリンゴを合わせて15個つめて、合計1700円になるようにしたい。
リンゴは何個つめばよいか。
方程式の文章題では求めたいものを文字でおくのが鉄則。
今回は、りんごの個数を求めたいからこいつをx個としよう!
ポイントは桃の数をxで表せるかどうかだね。桃とりんご合計15であることを使ってあげよう!
中3です。
【横の長さが縦の長さより4cm長い長方形の厚紙の4すみから、一辺2cmの正方形を切り取って、その残りの厚紙を点線に沿って折り曲げて直方体の容器を作ったら、容積が90cm3になった。元の長方形の厚紙の縦の長さを求めなさい。】
という問題を解く時、初めに
『元の長方形の縦の長さをxcmとすると、横の長さは(x+4)cm』
と書きました。しかし解答を見た所まだ続きがあり、
『容器の底面の縦と横の長さは、縦…□cm、横…○cm、高さは2cmだから、直方体の容器の関係から…』と書かれていました。ですが教科書の類題では、そこまで丁寧に書かれていませんでした。この問題は、初めにどう書くのが適切なのでしょうか?これに限らず、他の問題でも最低限どこまでかけばよいのかがよくわからなくて、、
>『元の長方形の縦の長さをxcmとすると、横の長さは(x+4)cm』
これでいいと思うよ!
あとは、まあ、直方体の体積で方程式を立てるからその道筋みたいなものだよね。
ぶっちゃけ答えがあってれば文句なしじゃないかな。採点する先生にもよるかもだけど
『ある数とその数の2乗との和は90です。
ある数を求めなさい。』
この問題が、全然わかりません。
宜しければ、解説をお願い致します。
>ある数とその数の2乗との和は90です。
ある数を求めなさい
方程式の文章題の鉄則は、求めたいものを文字でおくこと。
今回は、ある数を求めたいからこいつをxとおこう。
あとは、ある数の2乗をxで表して、そいつをxと足したら90になったっていう方程式作ればいいねー
連続する3つの正の整数があり、まん中の数の平方が他の2数の和を6倍した数に等しい。この3つの整数を求めなさい。 という問題を教えてください!
>連続する3つの正の整数があり、まん中の数の平方が他の2数の和を6倍した数に等しい。
この3つの整数を求めなさい。 という問題を教えてください!
真ん中の数をxとおいてみよう。
あとは、連続する3つの数をxで表してから、
「まん中の数の平方が他の2数の和を6倍した数に等しい」という等式を作ろう
先月回収したアルミ缶の個数は、回収した缶全体の3分の5より18個多かった。
今月回収した個数は、先月と比べて、アルミ缶が50個増え、スチール缶が20個減り、回収した個数はアルミ缶がスチール缶の2倍となった。
このとき、先月回収したアルミ缶と先月回収したスチール缶の個数をそれぞれ求めなさい。という問題を教えてください!
>先月回収したアルミ缶の個数は、回収した缶全体の3分の5より18個多かった。
今月回収した個数は、先月と比べて、アルミ缶が50個増え、スチール缶が20個減り、回収した個数はアルミ缶がスチール缶の2倍となった。
このとき、先月回収したアルミ缶と先月回収したスチール缶の個数をそれぞれ求めなさい
先月回収したアルミ缶をx個、先月回収したスチール缶の個数をy個としてみよう。
「先月回収したアルミ缶の個数は、回収した缶全体の3分の5より18個多かった」で1つ、
「今月回収した個数は、先月と比べて、アルミ缶が50個増え、スチール缶が20個減り、回収した個数はアルミ缶がスチール缶の2倍となった」
で2つ目の等式を作ってみよう。
和が15で、積が36になる2つの数がある。
一方の数をxとして、次の問いに答えなさい。
⑴xについての方程式をつくりなさい。
⑵これら2つの数を求めなさい。
という二次方程式の利用の問題です、、
⑴は解けたのですが⑵がごちゃごちゃになってしまいます。
解説お願いします!
>和が15で、積が36になる2つの数がある。
一方の数をxとして、次の問いに答えなさい。
⑴xについての方程式をつくりなさい。
⑵これら2つの数を求めなさい。
という二次方程式の利用の問題です、、
⑴は解けたのですが⑵がごちゃごちゃになってしまいます。
解説お願いします!
x(15-X)=36
になったかな?
これは左辺を分配法則で展開して、右辺に左辺のやつらを移項させて
因数分解の解き方で解いてみよう!
二次方程式の利用の座標の解説お願いします!
二次方程式の文章題がわかりません。
教えて下さい。
一の位と十の位の数の和が15である2けたの正の整数がある。この数の一の位と十の位の数を入れ替えた数ともとの数との積が6786です。
2数の積が6768であることに関して、方程式をつくりなさい。
いいね
よゆう〜