二次方程式の面積の文章問題ってどう解くの??
こんにちは!この記事をかいてるKenだよ。人生playhardだね。
二次方程式の利用では文章題がたくさんでてくるね。
連続する整数の問題とか、
動点についての文章題とかね。
もう、ほんとうに種類ありすぎ^^;
今日は、二次方程式の利用の文章題でよくでてくる、
二次方程式の面積についての文章題の解き方
を紹介していくよ。
よかったら参考にしてみて。
二次方程式の利用の面積の文章題の解き方4ステップ
つぎの文章題をといてみようか。
練習問題
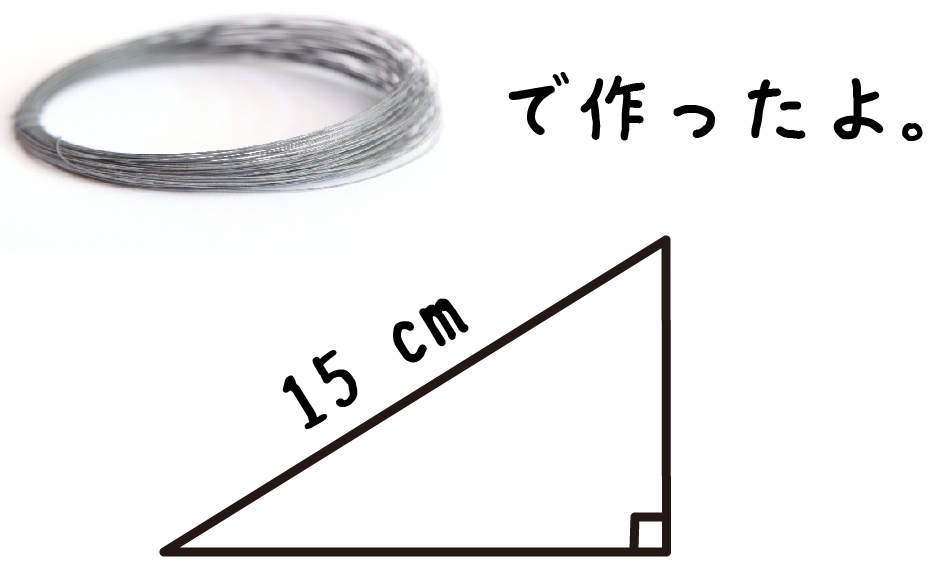
長さ30cmの針金で斜辺15cmの直角三角形を作りました。この三角形の面積が25cm^2になるとき、底辺と高さの長さを求めなさい。
Step1. 求めたいものを文字でおく
二次方程式の文章題の鉄則。
それは、
求めたいものを文字でおく
だよ。
どれを文字で置こうか迷わなくていい。
文章題が「だしてほしい」っていってるものを文字でおこうね。
練習問題では、
直角三角形の辺の長さ
を求めたかったよね??
ってことは、いったん、底辺をx [cm]とおいてみよう。

Step2. 二次方程式をつくる
二次方程式をつくろう。
文章題のどこかに、
○○○が△△△に等しくなるとき
ってかいてあるはずだ。
それをもとに、
○○○ = △△△
っていう等式をつくればいいのさ。

練習問題でいうと、
三角形の面積が25cm^2になるとき
ってところに注目してほしいね。
つまり、これは、
三角形の面積 = 25cm^2
っていう方程式がたてられそう。

ってことで、直角三角形の面積を計算してみよう。
長さ30cmの針金でつくったから、周りの長さは30cmだよね??
だから、残りの辺の「高さ」の長さは、
(針金の長さ)-(斜辺の長さ)- (底辺)
= 30 – 15 – x
= 15 -x
になるね。

よって、この直角三角形の面積は、
(直角三角形の面積)
=(底辺)×(高さ)÷2
= x (15-x)÷2
になるね。
練習問題では、面積が「25 cm^2」になるんだったね??
この通りに二次方程式をつくってやると、
(直角三角形の面積) = 25
x (15-x)÷2 = 25
になるね。

Step3. 二次方程式を解く
つぎは、二次方程式を解いてみよう。
因数分解をつかった解き方でもいいし、
めんどかったら解の公式をつかってもいいよ。
練習問題の二次方程式は、
x (15-x)÷2 = 25
だったね??
分数をふくむ二次方程式だから、分母はらってみようか。
両辺に2をかけると、
x (15-x)÷2 = 25
x (15-x)÷2×2 = 25×2
x (15-x) = 50
になるね。

左辺を展開して移項すると、
x (15-x) = 50
15x -x^2 = 50
x^2 -15x + 50 = 0
になるね。

んで、
因数分解して二次方程式をとくと、
x^2 -15x + 50 = 0
(x-10) (x-5) = 0
x = 5, 10
になるね。

Step4. 解を吟味する
二次方程式の文章題はといておわりじゃない。
解き終わったあとに、
その解が文章題として適切かどうか??
をチェックしなきゃいけないんだ。
練習問題では、
- x = 5
- x = 10
っていう2つの解がゲットできたね??
xを「直角三角形の底辺の長さ」とおいてた。
底辺のx = 5のとき、
直角三角形の高さは、
10cm
になるね。
うんうん。辺の長さが正の数だし問題ない。

んで、「x=10」の場合をおなじように考えてみよう。
底辺x = 10のとき、
直角三角形の高さは、
5 cm
になる。
うん、正の数になってるから適切だ。

こんなかんじで、二次方程式を解いたあともチェックが大事。
解が文章題の条件にあってるかたしかめてね。
まとめ:二次方程式の面積の文章題も解き方いっしょ!
世の中には、いろいろな二次方程式の利用の問題がある。
だけどね、ぶっちゃけ、解き方はどれもいっしょ。
- 文字でおく
- 二次方程式をつくる
- 二次方程式をとく
- 解の吟味
の4ステップでいいんだ。
ガンガン文章問題をといていこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






問題で
長さ30センチの針金で斜辺15センチの直角三角形を作る、
この問題の三角形は不可能ですね
確かにこれ無理だな・・・・