文字式の利用の解き方がさっぱりわからん!?
こんにちは!この記事をかいているKenだよ。うたたねが得意だね。
中2数学の「文字式の利用」はけっこうむずい。
ここでは、
文字式を利用して「すごいこと」をしなきゃいけないんだ。
ただ計算するだけじゃ許してくれない。
まったく、中2数学もきついね笑

今日は、中2数学の山場ともいえる、
文字式の利用の問題の解き方
を3ステップで解説していくよ。
つまずいたときに参考にしてみてね^^
文字式の利用の問題の解き方がわかる3ステップ
文字式の利用の解き方はたったの3ステップさ。
例題をときながらみていこう!
2つの整数が、偶数と奇数のとき、その和は奇数になります。そのわけを説明しなさい。

Step1. 数字を文字式であらわすっ!
問題文の「数字」を「文字」であらわしてみよう!

イメージでいうと、
「数字」っていう野菜を、
「文字」っていう包丁で切って「文字式」っていうカレーをつくるって感じw

えっ。ちょっと想像できないだって??w
それじゃあ例題をみていこう。

例題では「偶数」と「奇数」っていう2種類の数字がでてきたね。
こいつらを文字で表現してやればいいのさ。
m、nを整数とすると、
- 偶数 = 2m
- 奇数 = 2n +1
と文字式ができるね。
だって、偶数は2で割り切れる数だからね。
ってことは、ある整数を2倍した数ってことになるでしょ??
また、奇数は「偶数に1を足した数」だから整数を2倍して1を足せばいいんだ。
これで偶数と奇数という「数字」を、
m・nという「文字」であらわせたね^^
Step2. 言われたことを実際にやってみる。
文字式を使って指示されたことをやってみよう。
文字式の利用では、必ず、
数字の文字式をつかって何かしてみて??
っていうメッセージが込められているんだ。
よーく問題文を読み返してみよう!

問題文を読み直してみると、
「その和は奇数になります」
っていう文にメッセージが隠されていない??
そう。
そうなんだよ。
この文章では、
「偶数」と「奇数」を足してみて??
っていうダイイングメッセージが込められているんだ。
コナンでもきっと読み取ってくるだろう。
つまり、この問題では、
「偶数」と「奇数」をたして「奇数」になるよー
ってことをいってあげればいいんだ。
だから、まずはその2つをたしてやるのさ。
実際に「偶数(2m)」と「奇数(2n+1)」をたしてやると、
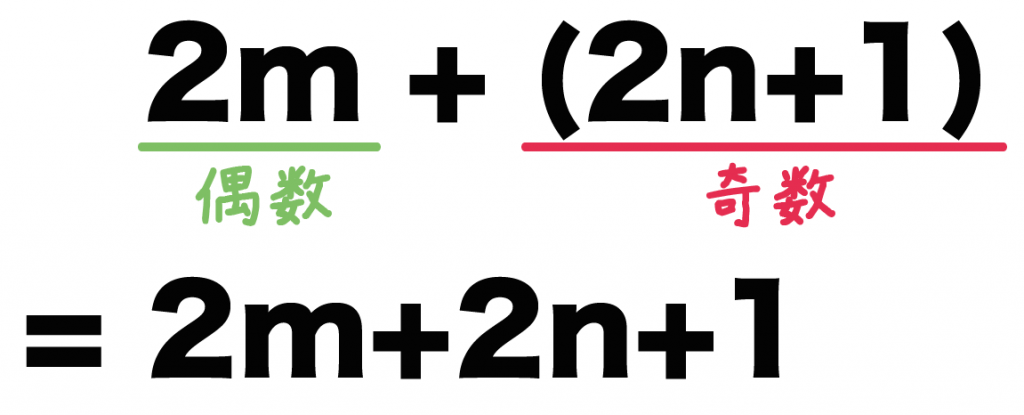
2m + (2n+1)
= 2m+2n+1
になるね!
Step3. ゴールに力技で着地する
あとは問題文の「ゴール」に力技で着地するだけさ。
問題文をよーく読んで、
何をすればゲームクリアなのか??
ということを見極めよう!
たいてい、メッセージ後に「ゴール」が潜んでいることが多いよ^^
例題の文章をもう1度読んでみよう。
すると、
「その和は奇数になります」
という文から、
「偶数」と「奇数」の和が「奇数」になること
がゴールだと読み取れるはずだ。

つまり、
偶数と奇数をたしたら奇数になる!
って言ってやれば問題でマルがもらえるってわけさ。
奇数ってことは、
整数×2+1
になってればいいよね??
2m + 2n +1
という文字式のmとnを係数2でかこってあげると、
2(m+n) +1
になるね。(m+n)は「整数+整数」で「整数」になるから、
2(m+n) +1 は「奇数」
ってことがいえるんだ。
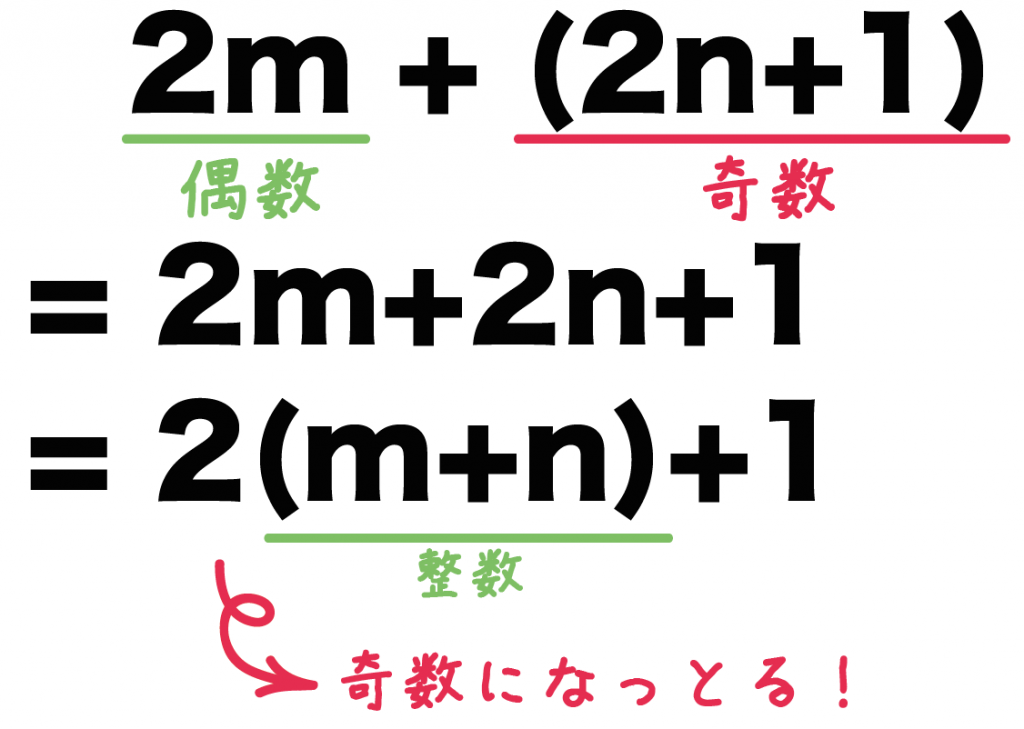
これで、問題のゴールの、
「偶数と奇数の和は奇数になる」
ってことがいえたわけ!
おめでとう^^
これで文字式の利用の解き方もゲットだね!
まとめ:文字式の利用の解き方は「ゴールの見極め」がカギ
文字式の利用の解き方は、
- 数字を文字式であらわす
- 言われたことをする
- ゴールに着地するためにへりくつを言う
の3ステップだったね。
この中でもっとも重要なのは、
問題文からゴールをみつける
ということ。
これさえできれば、どんな文字式の利用の問題でも大丈夫!
問題に慣れてテストをむかえてみてね^^
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。




そう言われてもやっぱりわからない!!もう少し詳しく教えてください!!
いいよ!どういう問題?!
私は文字式の利用の基本はわかるのですが応用になると解けません、応用の問題プラス解説or説明もわかりやすくお願いしま~す
明日が最後の期末なので。
ちなみに私は中一ですが・・・・・・・・・・・・・・・・
やっぱりわからないですね・・・
2m+2m+1など同じ文字を使って表してはいけない理由を教えてください
同じでも証明できればいいんじゃないかな
2つの整数が、ともに偶数の時、その和に、1を足した数は奇数になる。といった問題もありますがこの場合はどうすればいいのですか?
2つの偶数をそれぞれ整数m, nを使って表してみよう!
あとはそいつらを足して1を足すとどうなるか文字で表すだけさ
こんなに教えてもらったのにすみませんが、別の例題を出してください。
>>mana さん
仮にm=2にすると、
2m=4
2m+1=5
ですよね。
m=5なら、10と11です。
というように、同じ文字を使って2m、2m+1のように書いてしまうと、ある数2mとそれに1足した数との和についてしか説明ができません。
どんな奇数、偶数でも説明しなければならないので、違う文字を使って奇数、偶数を表さなければなりません。
連続する2つの奇数の和は4の倍数になる。
という問題の説明の式はどのようになるのでしょう??
>連続する2つの奇数の和は4の倍数になる。
という問題の説明の式はどのようになるのでしょう??
とある奇数を2n+1(nは整数とする)としたら、
もう一個の連続する奇数はnで表すとどうなるかな?
偶数と奇数じゃなく、偶数どうしや奇数どうしならおうしたらいいんですか。
>偶数と奇数じゃなく、偶数どうしや奇数どうしならおうしたらいいんですか。
やり方は一緒だよ!
とある整数を文字で置いて、2倍すれば偶数に、2倍したものに1を足せば奇数になる
正方形を一個作るには、棒が4本必要です。
棒を31本使ったとき、正方形は何個作れますか?
答えは、10個ですがその計算式を教えて下さい。
>正方形を一個作るには、棒が4本必要です。
棒を31本使ったとき、正方形は何個作れますか?
答えは、10個ですがその計算式を教えて下さい。
まっすぐに正方形並べるっていう条件はある??
そんな条件なかったら29本で11個作れたよ〜
奇数同士や、偶数同士での解き方も知りたいです!
どうしたら簡単に解けますか?
>奇数同士や、偶数同士での解き方も知りたいです!
奇数と偶数の表し方は同じ。
あとは足してどうなるかみてやればいいね
『6で割ると3余る数と、6で割ると5余る数の和は、6で割ると2余る数である。』
………という問題があるのですが、チンプンカンプンで全くわかりません。
教えてください。
>『6で割ると3余る数と、6で割ると5余る数の和は、6で割ると2余る数である。』
あまりが3の時の商をa、あまりが5の時の商をbとしてみよう。
あとは、その数をaとbを使って表してそれを足してみればいいんだ。
最後に6で()くくってみてー
文字式の利用なんですが、(a本の鉛筆をb人の子供に分けるのに1人に6本ずつ分けると4本足りない。bをaを使った式で表せ)という問題が分かりません。教えてくださいm(__)m
>a本の鉛筆をb人の子供に分けるのに1人に6本ずつ分けると4本足りない。bをaを使った式で表せ
1人6本ずつb人にくばると、6xbの鉛筆があればいいね。
でも、これよりは4本少ない本数が実際の鉛筆の本数aなんだね。この状況を等式で表してみよう
式の作り方とは関係ないのですが、式がわかっていても説明の書き方がいまいちなんですよねー。
教科書とかみてると、省けそうなところとか、
言い換えても良さそうなところをよくみかけます。
僕がいいたいのは、解答と少し違ってもいいか?と、
いうところです。最小限のとこかいて、伝われば
いいんでしょうか??よろしくお願いします。
分かりやすくて最高だぜー
>式の作り方とは関係ないのですが、式がわかっていても説明の書き方がいまいちなんですよねー。
教科書とかみてると、省けそうなところとか、
言い換えても良さそうなところをよくみかけます。
僕がいいたいのは、解答と少し違ってもいいか?と、
いうところです。最小限のとこかいて、伝われば
いいんでしょうか??よろしくお願いします。
言ってることが間違っていなければ、言い方は違っていても問題ないよ!
ただ、省きすぎると、解答を読む人がわからない時もあるから、丁寧に書いておくに越したことはないね
A@Bイコール2分のA➕B
とすると
(3@5)@7イコール?
となる。
この ?
の部分の求め方を教えてください
>A@Bイコール2分のA➕B
とすると
(3@5)@7イコール?
となる。
この ?
の部分の求め方を教えてください
計算のルールに従って地道に計算してやろう。
まずは()の中からだね
規則性の問題の解き方を教えてください。もうすぐ高校入試です。
>規則性の問題の解き方を教えてください。もうすぐ高校入試です。
規則性は公式とかがなくて問題ごとによるから、とにかく問題をたくさんといて慣れるのが大事。
難しすぎたら飛ばしてあとに解いてみよう
Q 連続する2つの奇数の和は4の倍数になる。このことを文字を使い説明せよ
という問題で私は2n+1+2n+1としたんですが、回答には2n-1+2n+1となっていました。
2n+1+2n+1ではないのはなぜですか?
>Q 連続する2つの奇数の和は4の倍数になる。このことを文字を使い説明せよ
という問題で私は2n+1+2n+1としたんですが、回答には2n-1+2n+1となっていました。
2n+1+2n+1ではないのはなぜですか?
2n+1が奇数になるのはオッケーだ。
あとはそいつを連続する奇数にしなきゃいけないね。
だから、2n+1の次の奇数(2を足して2n+3)にするか、1つ前の奇数(2を引いて2n-1)にしないといけないのね
「20kmの道のりを、はじめは時速3kmで、途中から時速4kmで歩いた。時速3kmで歩いた道のりをχkmとするとき、かかった時間の合計を求めなさい」という問題なのですが答えは、12分のx+5となっているんですが途中の式がわからないので教えてください。お願いしますm(-_-)m
長文すいません。
>「20kmの道のりを、はじめは時速3kmで、途中から時速4kmで歩いた。時速3kmで歩いた道のりをχkmとするとき、かかった時間の合計を求めなさい」という問題なのですが答えは、12分のx+5となっているんですが途中の式がわからないので教えてください。お願いしますm(-_-)m
時速4kmで歩いた距離をxで表してみて。
あとは時間を求める公式を使えばいいね
2つの奇数で
2n-1、2m-1でもいいんですか?
>2つの奇数で
2n-1、2m-1でもいいんですか?
使う文字は同じ方がいいね!
とても面白くて為になる教え方でした〜。
教えていただきたい問題はこちらです(*´꒳`*)
Y=5-4Xです(>人<;)
お願いしゃ〜す!❣️
>とても面白くて為になる教え方でした〜。
教えていただきたい問題はこちらです(*´꒳`*)
Y=5-4Xです(>人<;)
お願いしゃ〜す!❣️
グラフを描く問題かな?
切片を打って、あとはx=1の時のyを求めて2点を結ぶといいね
文字式ってほぼたしてけばいいんですか?
>文字式ってほぼたしてけばいいんですか?
今回の例題は足し算の答えである「和」を求めるから足したよ!
「差」とか「積」とか別のものを求めるんだったら話は違ってくる
3453のように、千、百、十、一の位の数をそれぞれa、b、c、dとおくと、a+b+c+d=3n(nは整数)である4桁の自然数は3で割り切れる。
成り立つ訳をa,b、c、dを用いて説明せよ。ただし、a、b、c、dはどのような値が考えられるか述べてから用いること。
↑教えてください!
>3453のように、千、百、十、一の位の数をそれぞれa、b、c、dとおくと、a+b+c+d=3n(nは整数)である4桁の自然数は3で割り切れる。
成り立つ訳をa,b、c、dを用いて説明せよ。ただし、a、b、c、dはどのような値が考えられるか述べてから用いること。
4桁の自然数をa, b,c,dでまずは表してみよう!
aを1000倍、bを100倍、cを10倍、それとdを足せば自然数になるはず。
あとは「a+b+c+d=3n」という条件を使えばいいね
テストでこんなむつかしい文章を全部書かなければいけないのは大変ではないですか
頭がゴチャゴチャになりますww
1ステップずつクリアしていこうぜ!
円錐の底面の半径を3分の1倍、高さを5倍すると体積は元の円錐の何倍になりますか。
という問題で答えが9分の5倍になっているのですがどうしてですか?
教えてください><
>円錐の底面の半径を3分の1倍、高さを5倍すると体積は元の円錐の何倍になりますか。
という問題で答えが9分の5倍になっているのですがどうしてですか?
こういう問題は実際に計算してみよう。
底面の半径をr、高さをhとして、元の円錐の体積、変更後の体積をそれぞれrとhで表せば良いね
これって何かもっと解きやすくするコツとかあるんでしょうか?塾の先生に聞いても暗記しろ、としか言われないので、、、
数学の証明のお作法になれるっていう意味では暗記したほうがいいね。そのうちなれるはず!
ただ、意味もなく暗記すると面白くないから、同じタイプだけどちょっと違う問題をたくさんといて、どのパターンがきても対応できるようにしよう
234のように、各位の数の和 2+3+4=9が3の倍数になっている3桁の自然数は、3の倍数である。
このわけを説明しなさい。
↑ごめんなさい!この問題がどうしても分からなくて、、
教えてもらえませんか?
百の位をa、十の位をb、一の位をcとしてみよう。
そして、
各位の和、自然数自体をabcを使って表してみよう
こんにちは勉強苦手な者です‼いつも見てます。
kenさんの例え方、とても面白いと思います。例えば、、、
「文字」っていう包丁で切って「文字式」っていうカレーをつくるって感じw
というところです。
とても面白いですよ。
いつも見てます勉強苦手な者です‼
kenさん。あなたの家を特定しました。(嘘)
良かったら返信お願いします。
数学のワークや教科書、などやっているんですがどうしても文字式の利用が無理です。教科書を見てノートにやっているのですが頭の中がぐちゃぐちゃになってしまって明日が定期テストの最終日で数学が……。でもkenさんの説明の仕方を見て、『なるほど…こういう感じでやればいいのか!』となりました。ありがとうございます!
なんかぴんときません
できればもう少し詳しく…
北朝鮮は、なぜ日本人をさらっているのか?
ゴールドエクスプリエンスはどのようにして生命を生み出していますか?
手と手の間に何らかのエネルギーを秘めているのはわかりますが、どのようなエネルギーですか?