数学の証明問題の書き方がわからん!?
こんにちは!この記事をかいているKenだよ。図書館、最高。
数学の証明はむずいよね??
雰囲気がめんどいのはもちろんだけど、
それ以上に、
証明の書き方がわからない!
からだと思うんだ。
だって、
先生ごとに書き方ちがうからね。
誰を信じたらいいのかわからなくなっちゃう。

そこで今日は、
【中学数学】3年間つかえる証明問題の書き方
って記事をかいてみたよ。
困ったときに参考にしてみて^_^
中学数学でつかえる証明問題の書き方
証明の書き方でおぼえてほしいのは、
型だよ。
ちまたではテンプレートともよばれてる。
そうだなあ、
クッキーを思い浮かべてほしい。
だいたい同じような形のクッキーが焼けるのって、
型があるからなんだ。
だから、
数学の証明でも「型」を使いこなせれば、
それっぽい証明が何個でもつくれることになるね。
数学の証明の型(書き方)って??
書き方の「型」はつぎのものだよ。
先生ごとによって書き方ちがうけど、
ぶっちゃけどれもこんな感じだ↓↓
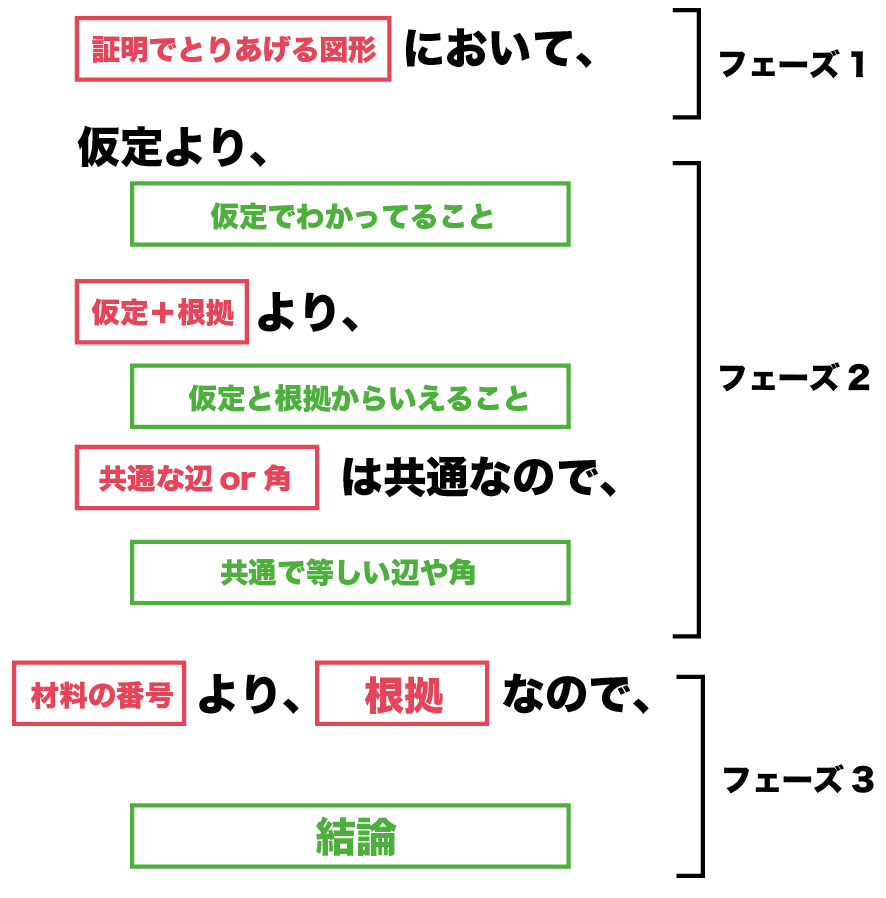
(証明でとりあげる図形)において
仮定より、
(仮定よりわかっていること)
仮定+根拠より、
(仮定と根拠からいえること)
(共通な辺or 角)は共通なので、
(共通で等しい辺や角)
(材料の番号)より、(根拠)なので、
結論
じつはこの型、
- 戦うフィールドを選択する
- 結論をみちびくための材料をとりあげる
- 結論をいう
っていう、3つのフェーズにわかれている。
この「型」で例題をといてみよう!
例題
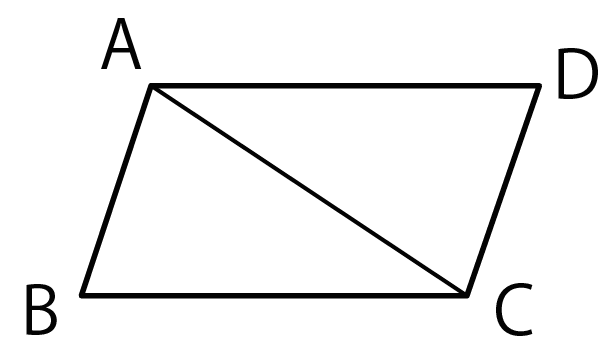
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、△ABC≡△CDA
を証明しなさい。
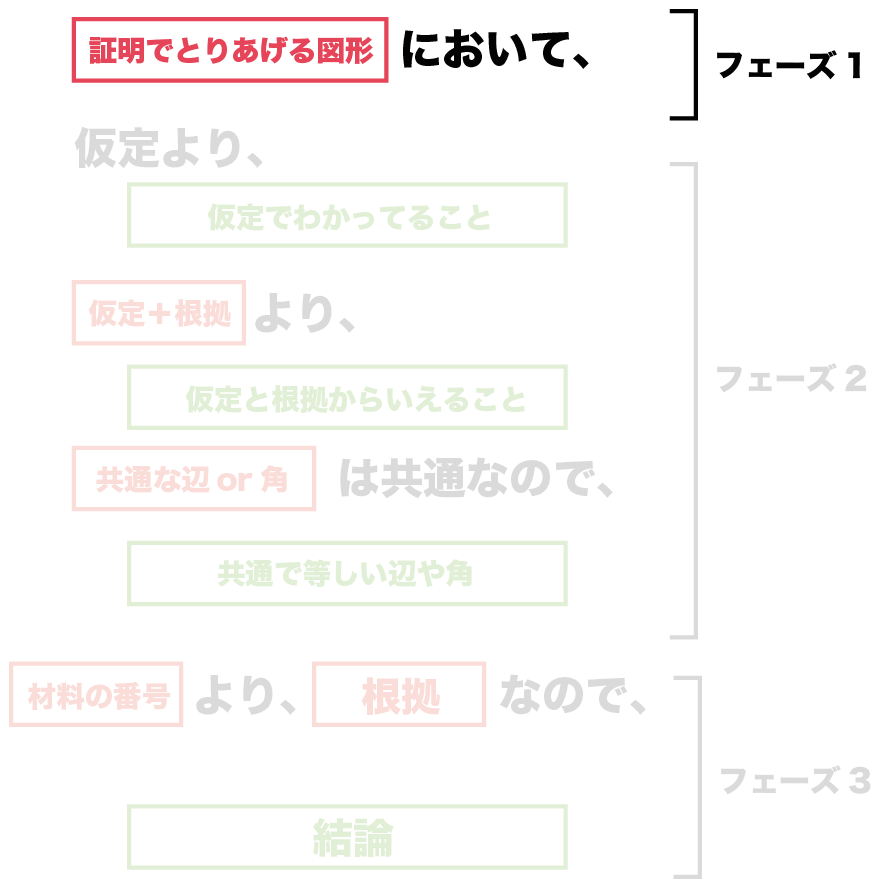
フェーズ1. 証明でとりあげる図形を宣言する!
書き方のいちばん最初は、
どの図形を証明でとりあげるのか??
を宣言することなんだ。
〜において
ってかいて、
「〜」には「証明でとりあげる図形」をかいてあげよう。
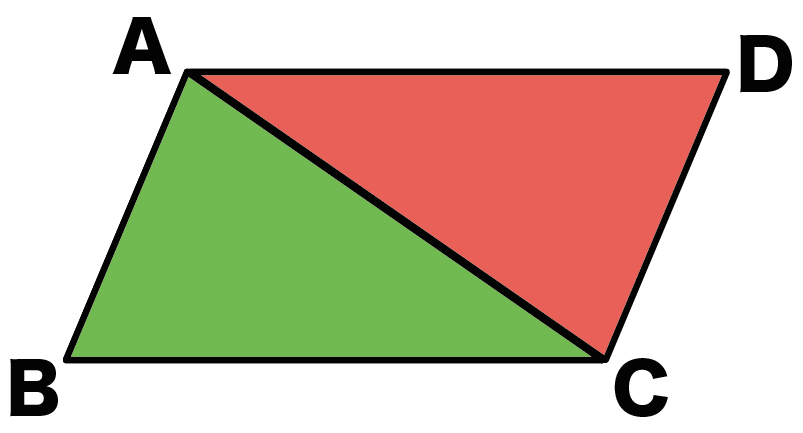
例題では、
△ABCと△CDAの合同を証明していくよ。
ってことは、この証明ではおもに、
△ABCと△CDA
の話をしていくことになるんだ。
だから、証明のいちばん最初で、
△ABCと△CDAにおいて、
って証明でとりあげる図形を宣言してみて!
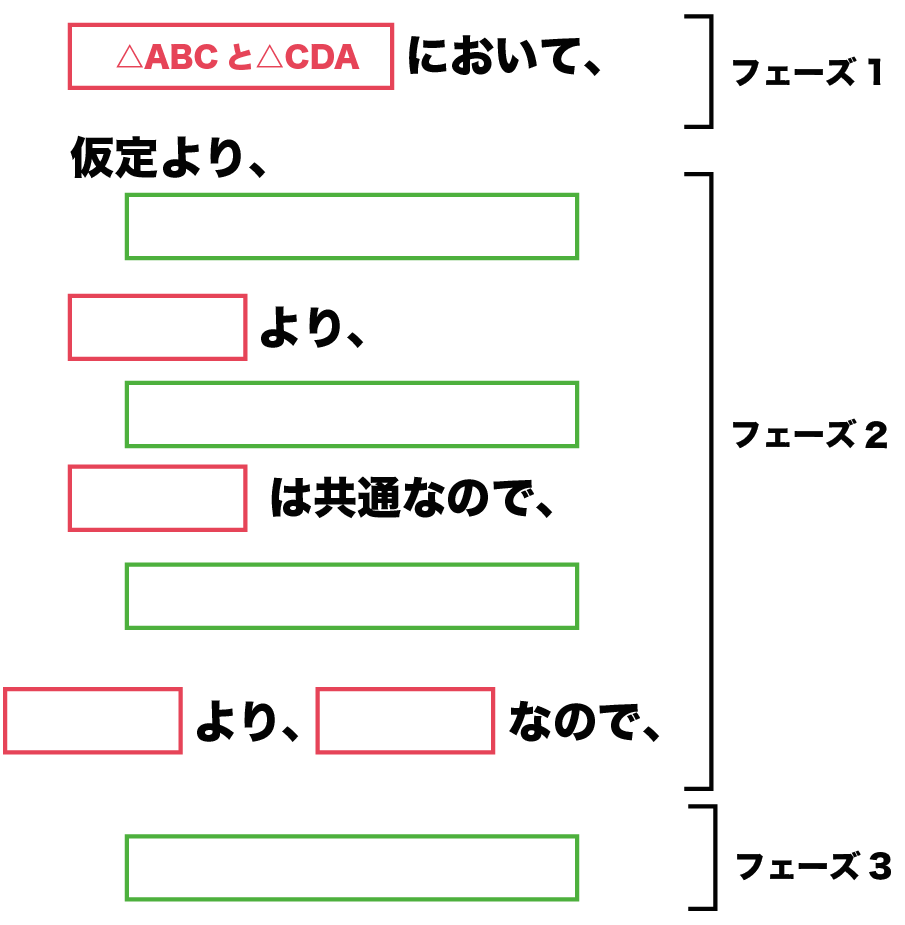
このフェーズはぶっちゃけ、
あってもなくても構わない。
だけどこいつをかいてやることで、
- 頂点の対応順のミスをなくせる
っていうメリットがあるんだ。
ぜひ、証明のいっちゃん最初に
「証明でとりあつかう図形」を宣言してみてくれ!
フェーズ2. 結論をみちびくための材料を羅列する
結論に必要な材料をならべるフェーズだ。
- 問題文でわかっていること
- それらからわかること
をどんどんかいていこう!
結論の材料の並べ方はつぎの3パターンがあるよ。
- 「仮定」より、+「仮定をそのまま」
- 「仮定+根拠」となることがらより、「仮定とその根拠からわかること」
- 「〜は共通」より、「共通となっている等しい辺や角」
このパターンをぜんぶ使わなくてもOK。
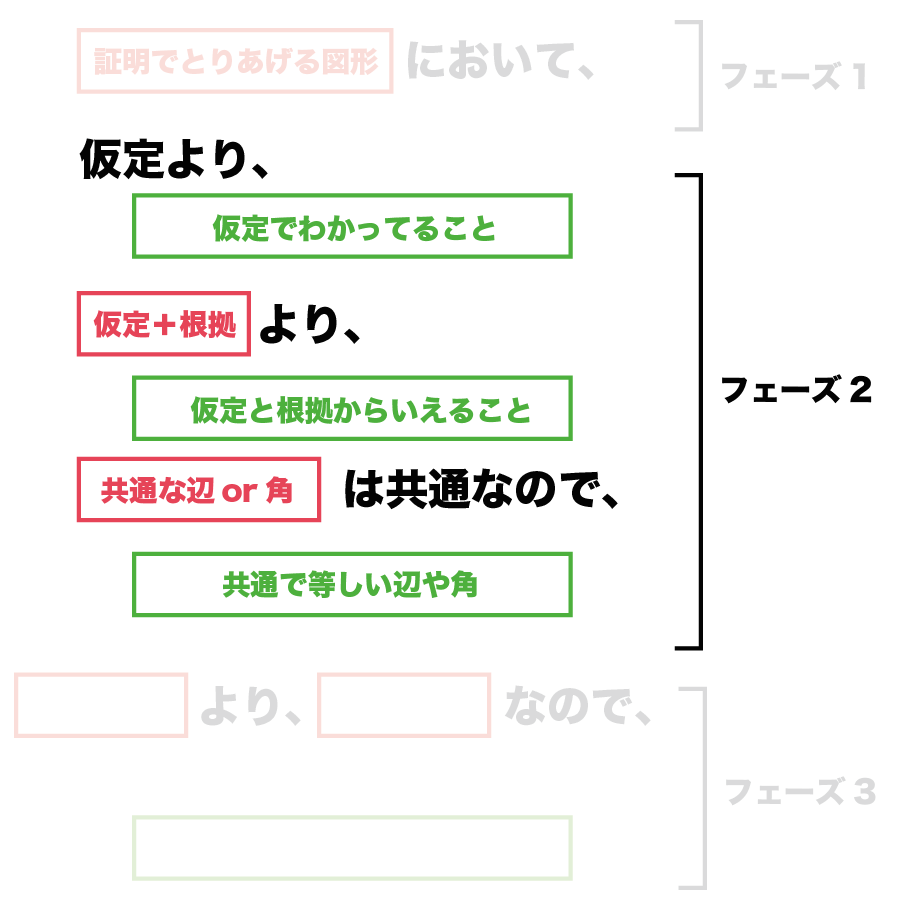
1つでも2つでも、ぜーんぶつかってもいいよ。
その証明に必要なものをチョイスしてみてね。
例題ではこんな感じになる↓↓
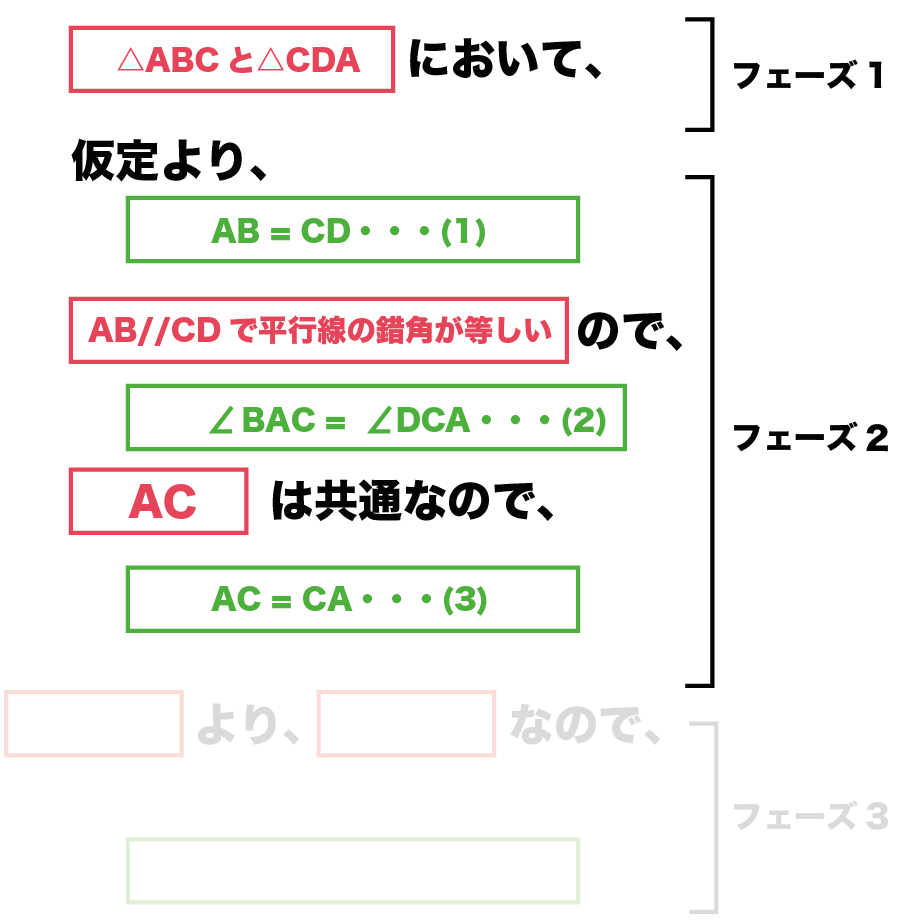
それぞれに番号ふるのを忘れずに!
フェーズ3. 結論をいったる!
最後はいよいよ結論。
フェーズ2で生み出した材料から、
結論(証明のゴール)
をみちびいてやろう。
書き方としては、
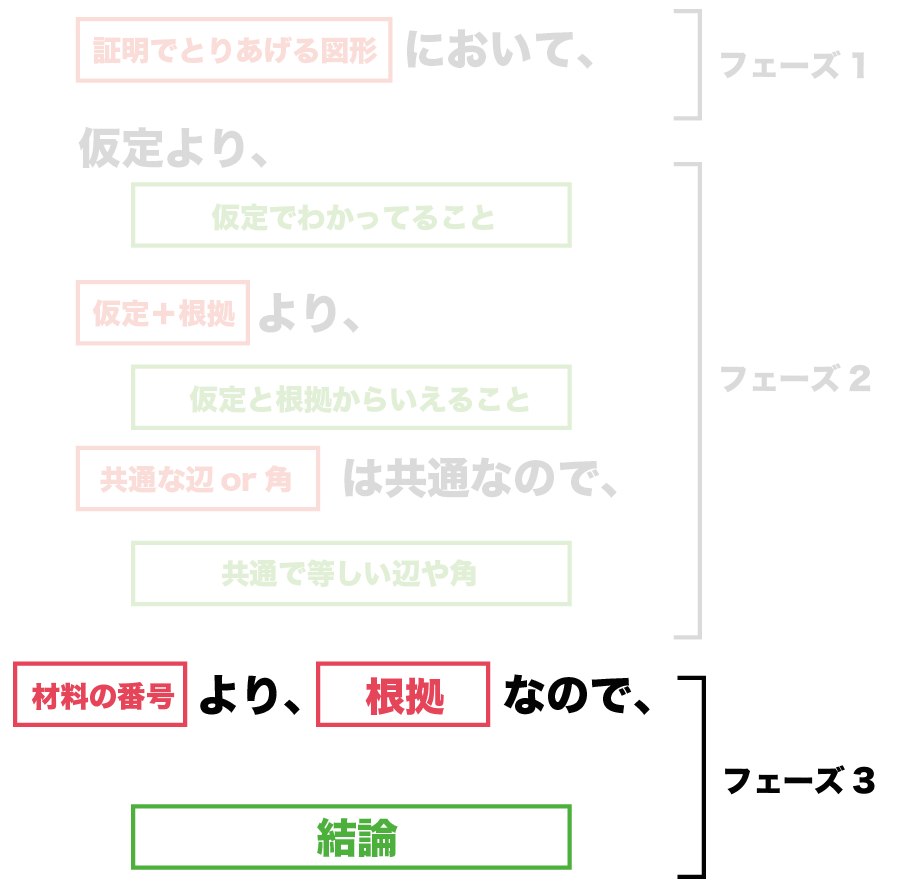
(材料の番号)より、(根拠のあることがら)なので、
(結論)である。
がのぞましいね。
例題でいうと、こうなる↓↓
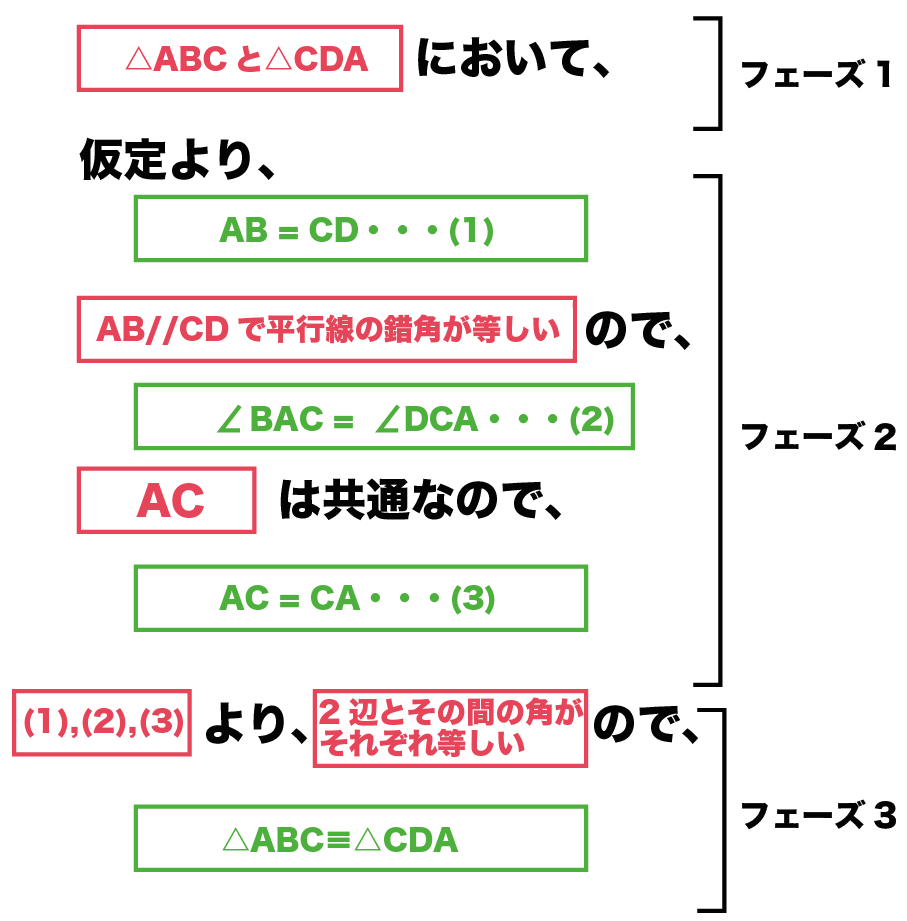
もし、結論が「角ABC = 角CDA」だった場合は、
もう一回フェーズ3をくり返してみてね。
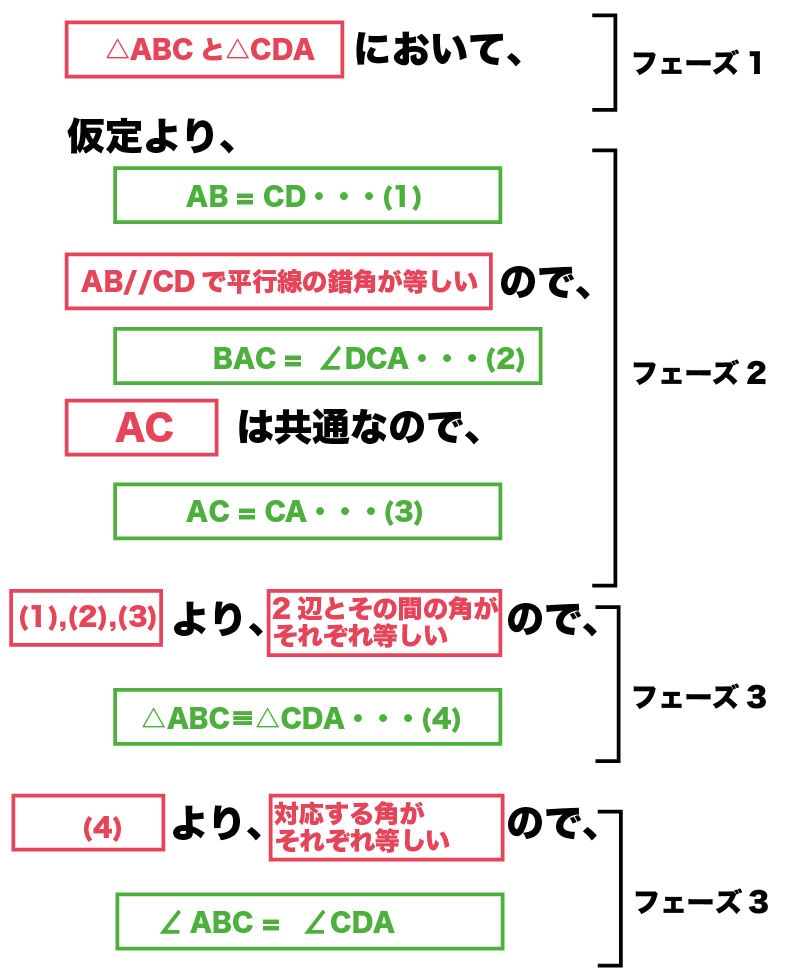
こんな感じで、問題によって、
フェーズ2や3が数回くり返すこと
もあるよ!
必ずしもこの型がピタリとはまるわけじゃないから、
気をつけてね^_^
まとめ:数学の証明は書き方おぼえればどうにかなる!
数学の証明はぶっちゃけむずい。
解き方もようわからん。
だけど、
書き方の「型」をおぼえてしまえば大丈夫。
それ通りにかいていくだけでいいからね!
問題をときまくって書き方になれていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







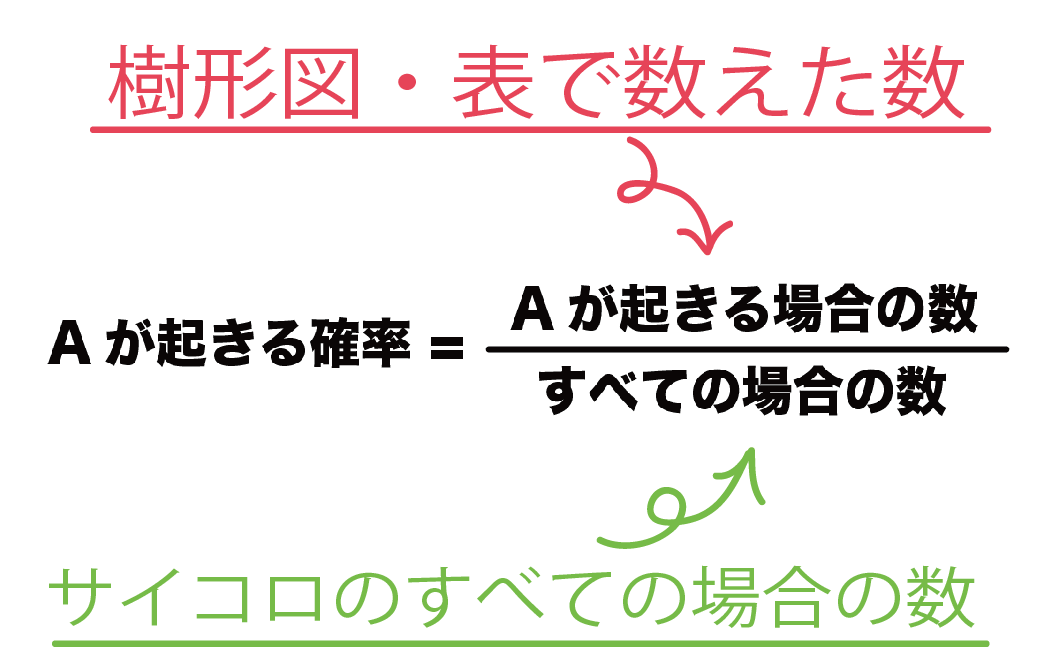
台形と三角形の組み合わせの証明の問題を解くためのカギはなんでしょうか?
問題送ってみて!
明日テスト頑張れそうです
ファイト〜
写真を使ってききたいんですが…
図がなくちゃ問題いってもいみなくないですかね?
>写真を使ってききたいんですが…
図がなくちゃ問題いってもいみなくないですかね?
言葉で質問してみて笑
証明に苦手意識を持ってしまうのですが、数をこなせばなくなりますか?
>証明に苦手意識を持ってしまうのですが、数をこなせばなくなりますか?
うん。数をこなすと書き方がわかってくるよ!
高校受験前なんですが証明が意味がわからないんですが
今からでもできる用になれますか?
>高校受験前なんですが証明が意味がわからないんですが
今からでもできる用になれますか?
まだ間に合う!
たくさん問題を解いてまずは書き方に慣れてしまおう
次の図のように、AB<AC、∠BAC=90°の△ABCがある。点Dは、点Aを通り辺BCに平行な直線上の点で、∠ADB=90°である。また、点Eは、辺AC上の点で、BA=CEである。点Fは、辺BC上の点で、BC⊥EFである。
A
D | ̄ ̄ ̄  ̄  ̄/ \E
| / | \
| / | \
| / | \
B |/___________ |______ \C
F
>次の図のように、AB
受験まであと3ヶ月もなくて、、。
とても焦ってます(T ^ T)
受験までに、できるようになりますか??
まだ3ヶ月もある!!
落ち着いて残りの期間できることを積み上げていこう
今中二です。一日何時間勉強したら、受験に間に合いますか?
>今中二です。一日何時間勉強したら、受験に間に合いますか?
まだ1年間もある!目指すレベルとか現状にもよると思うけど、今日から積み上げていくしかないね
受験生です。
今から偏差値を少しでも多く上げたいのですが、効率の良い勉強の仕方を教えてください。
数学が全く分かりません。
相似を教えて下さい!
「〜において」や、「〜は共通なので」のような最後ではないのを教わったのですが、どちらが正しいのでしょうか?
>受験生です。
今から偏差値を少しでも多く上げたいのですが、効率の良い勉強の仕方を教えてください。
今の時期は実践的な過去問や模試の問題にチャレンジして復習するサイクルを回すのがいいんじゃないかな!
基礎がまだできてないと感じたら戻ってみよう!
>数学が全く分かりません。
相似を教えて下さい!
まずは「相似比の求め方」を押さえよう!
>「〜において」や、「〜は共通なので」のような最後ではないのを教わったのですが、どちらが正しいのでしょうか?
証明の書き方は人それぞれ。言ってることが間違ってないければ大丈夫!
先生が教えてくれた書き方をマスターすればいいよ!
受験生です。
三角形はできるようになったのですが、
四角形の方の証明がよくわかりません(汗)
分かりやすいやり方を教えてください!
>受験生です。
三角形はできるようになったのですが、
四角形の方の証明がよくわかりません(汗)
分かりやすいやり方を教えてください!
基本は同じだ!
ただ、四角形の証明はおそらく、平行四辺形やひし形であることを証明しなさいっていう問題だろうからちょっと書き方はことなるよね。
その場合、冒頭で別に合同を証明する三角形を宣言しなくてもいいけど、最後は合同条件を使う代わりに平行四辺形になる条件などを書くことになるかな
最後のフェーズ3のところは、「平行四辺形の2組の対辺は等しい。」の時も、△ABC=△ADCなんですか?
>最後のフェーズ3のところは、「平行四辺形の2組の対辺は等しい。」の時も、△ABC=△ADCなんですか?
結論は場合によって変えて大丈夫。
その場合、根拠を添えて「平行四辺形の2組の対辺は等しい。」といえばいいね
直角三角形の合同がわかりません
>直角三角形の合同がわかりません
まずは直角三角形の合同条件から覚えてみよう
途中で角同士の引き算とかが入る証明がわからないです!
やりやすい方法教えてください!
>途中で角同士の引き算とかが入る証明がわからないです!
やりやすい方法教えてください!
問題送ってみて!
△ABCと△ECDは正三角形です。
AD=BEであることを説明しなさい。
↓
正三角形が二つあって、AからDに線が引いてあってEからBにも線が引かれてます。
解き方教えてください
>△ABCと△ECDは正三角形です。
AD=BEであることを説明しなさい。
↓
正三角形が二つあって、AからDに線が引いてあってEからBにも線が引かれてます。
解き方教えてください
△ACDと△BCEの合同から、対応する辺の長さが等しいことを証明するよ。
ポイントは角ACDと角BCEが等しいことを言えるかどうかだね。
証明の仮定の根拠ってどんなのがあるんですか❓
相似の証明で仮定が書いていないのはどうしたらいいんですか!笑
>相似の証明で仮定が書いていないのはどうしたらいいんですか!笑
何かしら書いてあるはず!笑
明確に仮定として触れられていなくても、図形の形なんかがわかってるとしたら(例えば平行四辺形)それも仮定のうちだね
中2です
私の学校の先生はよく三辺相当などの言葉を使うのですが、これと似た様な言葉を他にも教えて頂だけると嬉しいです!
>私の学校の先生はよく三辺相当などの言葉を使うのですが、これと似た様な言葉を他にも教えて頂だけると嬉しいです!
そのほかにも、
・二辺夾角相等(2組の辺とその間の角がそれぞれ等しい)
・二角夾辺相等(1組の辺とその両端の角がそれぞれ等しい)
があるよ〜
わかりやすいです!
ありがとうございます
平行四辺形の性質で、平行四辺形になるための条件に似たような定理があって覚えられません。定理などの覚え方、区別の仕方などありますか?
証明がわからん
>平行四辺形の性質で、平行四辺形になるための条件に似たような定理があって覚えられません。定理などの覚え方、区別の仕方などありますか?
平行四辺形の定義、平行四辺形の性質、平行四辺形になるための条件の順番で覚えるといいよ。
なぜなら、性質は定義を含んでいるし、条件は性質を含んでいるからね
>証明がわからん
たくさん問題を解いて数学の証明の形式に慣れていこう。
慣れていくとどんどん問題が解けるようになるよ
分かりやすい!!
ありがとうございました
明日テストなんですけど証明分かりません
理解ができない…なんでみんな理解できるの?先生に聞いてもわかんないし、答えとか解説とかみても理解ができないから問題が解けない。
>明日テストなんですけど証明分かりません
一問でもいいから証明問題を解けるように何度も練習しておこう
>理解ができない…なんでみんな理解できるの?先生に聞いてもわかんないし、答えとか解説とかみても理解ができないから問題が解けない。
人生で初めての経験だから最初は戸惑うのは当然。
証明自体に慣れる必要があるから、めげずに挑み続けてみよう
証明の問題を早く得コツとかってありますか?
小テストのときにいつも全証明が4問以上出るので教えてください!
>証明の問題を早く得コツとかってありますか?
小テストのときにいつも全証明が4問以上出るので教えてください!
やっぱ練習しまくるしかないね。証明の問題は途中過程を書かなきゃいけないから、近道はないね
明日証明できる穴埋め一問、完全回答一問ですが、何がなんだかわかりません‼
>明日証明できる穴埋め一問、完全回答一問ですが、何がなんだかわかりません‼
穴埋めの時は合同や相似の対応する頂点の順番を間違えないようにしよう!
穴埋め対策でも自分で一から証明できる力がある心強いね
分かりやすかったです。ありがとうございました。
これで明日の受験も少し不安がなくなりました
ありがとうございます
よかった!!^^
証明の先生とかが証明の部分部分につけるあの 」 って何ですか?
教えてください!
あれは証明終わりって意味だよ!
記号使うとかっこいいからな!
結婚してますか?
どう思う?
ほかの証明も分かりやす教えください今回のは分かりやすかったです
証明で、①~⑥くらいまで出てくる証明があるのですが、具体的にどうすれば、うまく①や④などを使いこなせますか?
数字を振るのはあくまでも証拠に番号をつけるだけであって、
まあ、別に後で使わなくても大丈夫
このやり方は、すべての証明に対応していますか?
上の例題の四角形の平行線の錯角の2つはどこにあるんですか?
角BACとDCAじゃないかな!
試してみます!
明日テストなので。
参考になりました!
ありがとうございます。
わかりやすくて、参考になりました。
明日テストなので、ノートに丸写ししてしまいました。
いい点数取れるか楽しみです。‼️
とってもわかりやすかったです♪
ありがとうございました
明日のテストがんばります‼️
ken 先生‼︎
数学の証明問題を好きになる
方法を教えて頂きたいのですが…
どうしたら好きになれますか?
解けるようになると好きになるはず!
ってことで、やり方に慣れるまで耐え忍びながら問題を解きまくろう!
数学の証明が少しだけだけど分かりました‼ もっと好きになるためにたくさん勉強します‼
授業より分かりやすくて助かりましたm(_ _)m
ありがとうございます!!!
明日テストなんですが、ken先生とても分かりやすかったです!
ありがとうございます!これで少しでも出来るようになりました!