連続する3つの整数の和が3の倍数になるってほんと!?
こんにちは!この記事をかいているKenだよ。おしぼりは無敵だね。
文字式の利用で、
連続する3つの整数の和の問題
ってでてくるよね。
たとえば、つぎの問題 ↓↓
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする。
日常生活では3つの整数の和なんて考えないよね??
だって、必要ないもん。
でもね、中2数学の問題ではよくでてくる証明なんだ。
今日はこの問題を攻略してみよう!
連続する3つの整数の和の証明がわかる4ステップ
4ステップで証明できちゃうよ。
- nを整数とする
- 連続する3つの整数をnであらわす
- たす
- さけぶ
さっきの例題をといていこう!
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする
Step1. 整数をnとする
ある正の整数を「n」としてみて。
nは「正の整数」だから、
1にもなるし、2にもなるし、10にだってなるんだ。
えっ。なぜ「n」を使わなきゃいけないんだって?!
えっ?
zを使いたい??
じつは、nは英語の「number (数字)」からきているんだ。

ぶっちゃけzとかqでもいいんだけどさ。
nをつかうとカッコいいじゃん?笑
とりえあず正の整数を「n」とおこう!
Step2. 連続する整数をnであらわす
連続する3つの整数をnであらわそう!
連続する3つの整数ってたとえば、
1, 2, 3
みたいに、1ずつ違う整数のことだ。

たとえば、
1, 4, 5
とかは連続してないね。
だって、1ずつ離れてないし。

nであらわすときは、
連続する3つの整数のうち、正の整数nを、
真ん中の整数
とおくといいよ。

そうすると、
- 一番小さい整数
- 一番大きい整数
をnで簡単にあらわせるからね。
連続する3つの整数は1ずつ離れてる。
よって、
- n-1
- n
- n+1
になるはずだ!

Step3. たす
つぎは、連続する3つの整数をたそう。
nであらわした、
- n-1
- n
- n+1
をたせばいいんだ。
ぜんぶたしてみると、
(n-1)+n+(n+1)
= 3n
になるね!
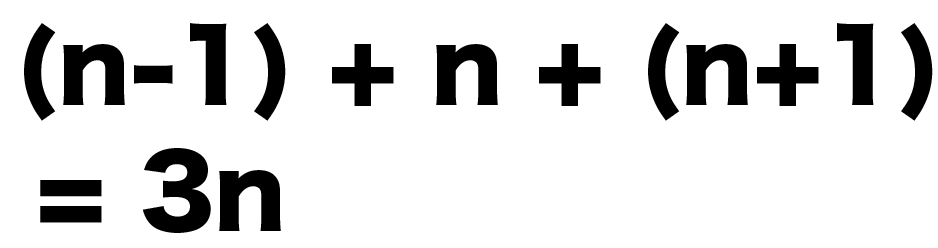
Step4. 和が3の倍数になると証明する
最後に、和が「3の倍数」になる証拠をみつけよう。
証拠がみつかれば、
連続する3つの整数の和が「3の倍数」である
って証明できるからね。
例題でいうと、
連続する3つの整数の和は、
3n
になったね。
で、nは正の整数だったよね??
ってことは、
3n
は3の倍数になるんだ!

だって、「n」には1とか2とか6とかがはいるわけだからね。
そいつらが3倍されたら、
- 1→3
- 2→6
- 3→9
3の倍数になるじゃん??

だから、連続する3つの整数の和は3の倍数っていえるんだ!
まとめ:連続する3つの整数の和は3の倍!
この問題は、
- 正の整数をnであらわす
- 連続する整数たちをnであらわす
- たす
- さけぶ
の4ステップで証明できちゃう。どんどんチャレンジして行こう
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






「1,3,5,7のような連続する4つの奇数のうちの2番目に小さい数をnとするとき、4つの奇数の和をnを用いた式で表しなさい。」
よくわかりません。解説で、{4つの奇数はn−2,n,n+2,n+4と表せる}とあったのですが…何故そう表せるのでしょうか(_ _)
>「1,3,5,7のような連続する4つの奇数のうちの2番目に小さい数をnとするとき、4つの奇数の和をnを用いた式で表しなさい。」
よくわかりません。解説で、{4つの奇数はn−2,n,n+2,n+4と表せる}とあったのですが…何故そう表せるのでしょうか(_ _)
奇数をnとすると、その次の奇数は、次の偶数の次だから+2しないとね。
逆に、その前の奇数だったら前の偶数の前だからー2するんだ
xの3乗たすyの3乗
yの4乗たすxの4乗
の考え方(展開の方法?)を教えてください
質問ではないんですけど、すっごくわかりやすかったです!!
助かりました! ありがとうございます!
ありがとう!頑張ろうぜ!!
てんさいや!!!!!!!!
ありがとう笑
0は倍数に入りますか?
(もし、nー1で、nが1の時、0になりますよね…)
あと、nの数字が小さかったりして(1とか)、n-2などがマイナスになる場合があると思うんですけど、マイナスになる場合も倍数ですか?
この問題だと正の整数という条件があるから0や負の数は含まれないかな!
似たような問題なんですが、
奇数から始まる3つの続いた整数の和が6の倍数になる…という問題で躓きました(˙꒳˙ )
整数をnにして式を作って足したんですが、その答えが6n+6になりました。ここまではいいのですが、この6n+6が6の倍数の形にするために6(n+1)になるらしく、どうして6n+6が6(n+1)になるのかのか分かりません。
どのように式を変形させたのでしょうか?
実力テストが近いので焦っています…:(;゙゚’ω゚’):
解説よろしくお願いします。
これは共通因数でくくるってやつだね。
分配法則を逆にしたものだ。
2つの項の6nと6は両方6がかけられているよね?
だからその共通の6でくくってやると6(n+1)になるんだ。この変形はよく出てくるから違うパターンでもマスターしておこう
助かります
連続する3つの奇数の和は3の倍数であって、6の倍数ではないことをを説明してください。
最も小さい整数をnにする場合の説明をお願いします。
プリントの参考になりました!!
良く良く分かった気がするうううぅぅぅぅ
頭いい