【中1数学】方程式でなんで移項ができるの？？

方程式でなんで移項ができるんだろう？！？

こんちゃー！イヌの散歩にはまってるKenだよー！

中学1年で勉強する「方程式」。ここで一番の疑問って、

なぜ移項することができるのか！？？

ってことだよね。今日は移項とは何か？？　という基礎的なことを振り返りながら「移項ができる理由」を振り返ってみよう！！

~もくじ~

1. 移項とは何か？？
2. 移項はなぜできるのか？？

方程式の鍵である「移項」って何？？

中1で勉強する「1次方程式」をとくために便利な「移項」というワザ。いったいコイツは何者なんだろうか。

まずは移項の正体をあばいちゃおう。

数学の教科書をみてみると「移項」って次のように定義されてるんだ。

等式では、一方の辺の項を、符号を変えて、他方の辺に移すことができます。このことを移項するといいます。

この移項を図をみながらゆっくりみよう。

「一方の辺の項」

を、

符号を変えて、

他方の辺に移す。

これが移項なんだ。

つまり、

等式では、

項を左から右に移動させてもいいし、右から左に移動してもいいんだ。ただし、符号は変えてね^^

これが方程式で重要となる「移項」の意味なんだ。

しっかり頭にぶちこんでおくれ！

なぜ移項なんてワザができるのか！？

それじゃあ、なんで移項って超能力ができるんだろうか！？　左から右へ符号を変えるだけで項が運べるなんてエスパータイプのポケモンみたいだよね？？？

じつは移項って「等式の性質」を使っているんだ。

※　等式の性質にイマイチピンとこないときはこの「等式の性質の記事」で復習してくれ^^

さっきの例では等式の性質の1つである、

「両辺から同じ数をひいても等式は成り立つよっ」

っていうものを使っているよ。

ためしに、

5x + 17 = 32　という等式の左と右から「17という数」をひいてみよう！

すると、

こうなる。

そんで、左の17-17がゼロになるよね！？

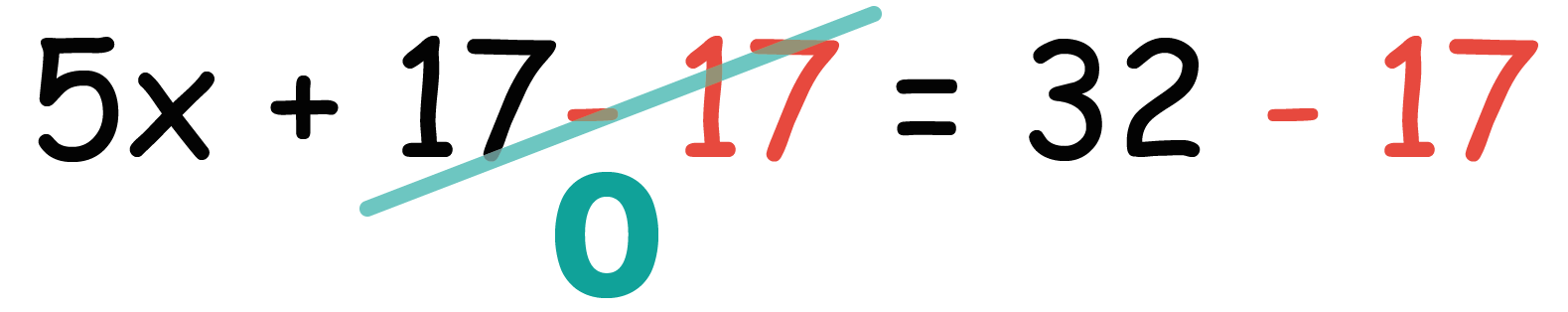
だから、

17という項があたかも「移項」したように見えるわけ。

移項って左から右に移すときに符号を変えるだけ。

だから、ものすごく簡単に感覚的にできちゃうんだ。だけれども、一番大切なのは、

なぜ移項ができるのか？？

ということを理解していること。これにつきる。

方程式をすばやく解くことも大切だけど、仕組みをわかっていることも同時に大切だよ。覚えておこう！！

移項もこれでスッキリ！！

方程式のかなめの「移項」についてスッキリしたかな？？　まだわからないときは、等式の性質を復習してもう一度移項を再現してみよう。

ゆっくりやればきっとわかるはず！

移項をつかって方程式をガンガン解いていこうー！

そんじゃねー^^

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。