【中学数学の基礎】正の数・負の数でおさえるべき4つのポイント

中学数学の「正の数・負の数」はマサラタウン？？

中学数学で一番はじめに乗り越えなければならない壁。

それが「正の数・負の数」という数学単元です。中学数学の最初の関門だけあって、かなりなめている生徒の方が多いのではないでしょうか！？

はあ？　正の数？？　負の数？？？　あんなの数学でもねえよ！

そんな挑戦的な態度を中学数学に叩き付けてくる方もいるかもしれません。ただ、この「正の数・負の数」という最初の数学単元をなめていると、とんでもなく痛い目に会う可能性があります。中学数学の基礎がゆえに、何度も復習を重ねねばならない単元なのです。

そこで今日は中学数学の最初の単元である「正の数・負の数」で理解するべき4つのポイントをわかりやすく解説していきます。部活とかクラスの人間関係で疲れている中学生！この記事を読んで中学数学を復習してから睡眠をとるようにしましょう！

正の数・負の数でおさえるべき4つのポイント

「正の数・負の数」で理解すべきポイントを4つ紹介していきます。

Point 1. 　「負の数（マイナス）」の定義を抑える

正の数・負の数でおさえるべき1番目のポイントは「負の数」について。小学校で散々習ってきた算数には正の数（＋の数）は当たり前のように出現してきました。つるの足の数を数える時も、亀の甲羅を数えるときも、ポケモンの名前を覚えるときも、必ず正の数をつかってきましたね。

誰一人として、

き、昨日は-9匹のポケモンをゲットしたぜ！！

と叫びません。いくらポケモンマスターでもそんな失態は犯さないでしょう。

しかし、中学数学ではこの負の数をいきなり使いこなさなくてはいけません！高校へ行っても大学へ行っても社会人になっっても、このマイナス（負の数）は知っていないと話になりません。中学数学の入り口で負の数の定義をしっかりと抑えておきましょう。

負の数とは何か？？　これをWikipediaで確認してみると、

0より小さい実数である。

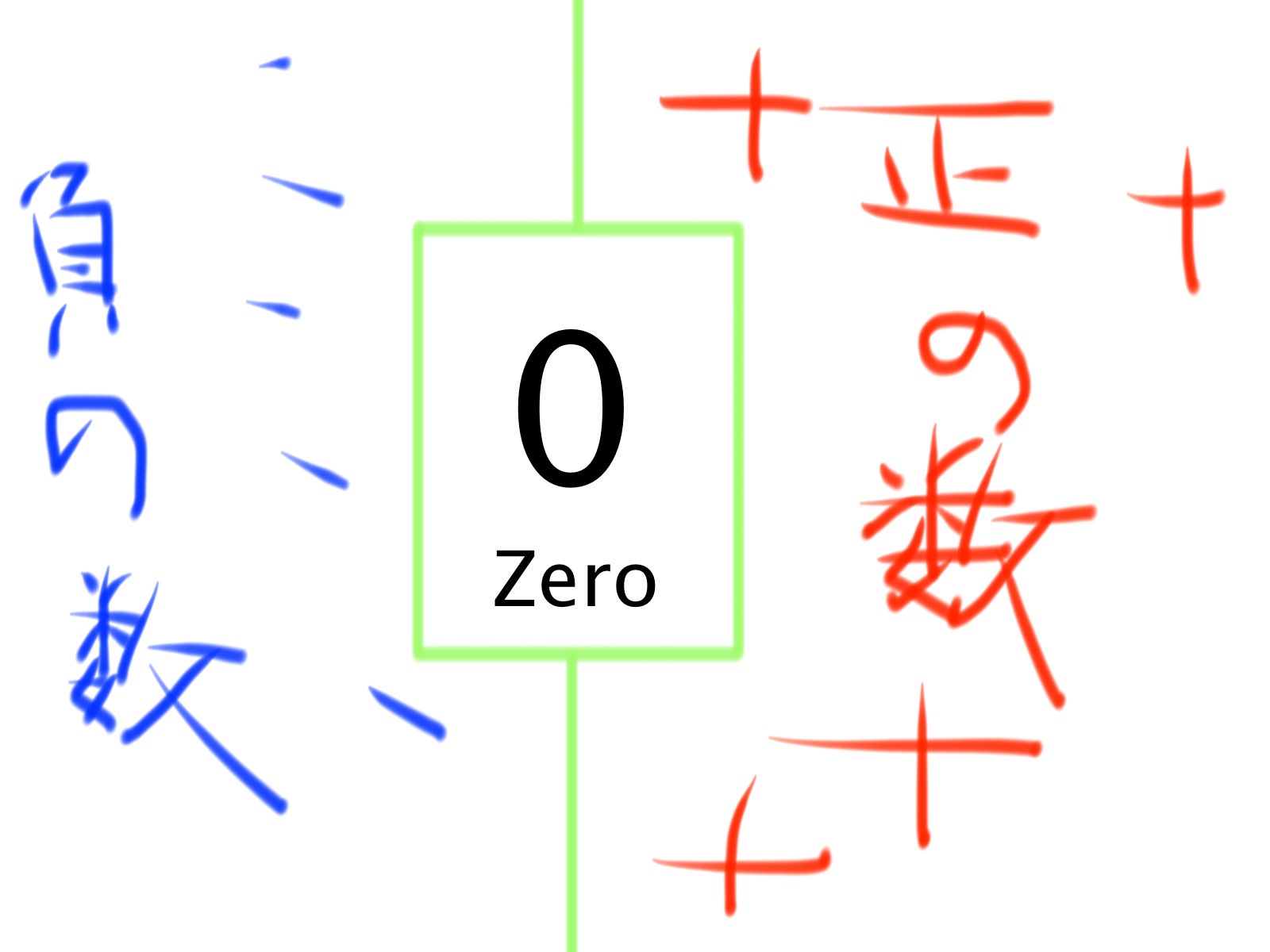
0を境に正の数と負の数が仕分けされている。つまり、0より0.0000001でも大きかったら正の数。0.000000009999でも小さかったら負の数になります。この「0（ゼロ）」が正の数・負の数の境界線になっていることに注目してくださいね。

板書きたねえー笑

Point 2. プラス記号を省略できる理由

負の数を学習する際に１つだけ知っておくべきことがあります。

それは、マイナス記号を省略できないということです。つまり、負の数の「-8」という数字を表現したい場合、「マイナスハチ」とか「8」のように「マイナス記号（-）」 を省略することができないのです。これは非常に見落としがちな点。

一方、プラスの記号はどうなのでしょうか？？　じつは＋記号に関しては省略する事ができます。

8という数字を、「+8」と表記することができるし、「8」とシンプルに記号を省略することができます。

えっ。それでは何故負の数の記号を省略できなかったのでしょうか？？？

その理由は、

負の数を表現する方法が「-」という記号１つのみだからです。これ以外に手段がないゆえに、マイナス記号を使わざるを得ないのです。

Point 3. 数直線の決まりごと

中学数学の最初の単元「正の数・負の数」では、負の数の説明によく数直線が用いられます。数直線とは、正の数と負の数の関係性を図で表現したもの。たとえば、こんな感じです↓↓

この数直線をすんなりと理解するためのポイントは「左右の大小関係」を把握することです。一体、誰が決めたのかわかりませんが、数直線では「ゼロより左が負の数」、「ゼロより右が正の数」という決まりがあります。ゼッタイにその逆の数直線は存在し得ません。これは地球が右回りに自転する自然現象と一緒。その事実に理由はないのです。

左は負の数、右は正の数

ということを頭に叩き込んでおきましょう。

Point 4 . 絶対値へのゼッタイ的な理解

最後にこの節で大切なことは「絶対値」をゼッタイに理解することです。教科書通りに絶対値を理解すると、

ゼロ（原点）からの距離

ということになります。これはシンプルでわかりやすい。しかし、もっと面白くて笑える絶対値の捉え方があってもいいのではないでしょうか。そこでぼくは個人的に絶対値を「木村拓哉」と「モテナイ男（ぼく？笑）」を例にとって考えてみました。

木村さんはご存知の通り、世の中の女性から「抱かれたい男ランキング1位」として選出されています。何年も連続で。そんな二人のイケメン度合いを数直線にとってみると、

こうなります。両者のイケメン度合いの開きはじつに、１５。なぜなら、モテナイ男が-9、キムタクが6のイケメン度合いを獲得しているからです。正の数・負の数という整数の観点からみれば、この両者の勝負はキムタクの圧勝でおわります。

がしかし、しかし。

ここで絶対値というスケールを使ってみましょう。絶対値とは「原点０からの距離」でしたね。

あるモテナイ男の絶対値　=  9

キムタクの絶対値　=  6

となります。つまり、このことからわかるのは、モテナイ男のほうがキムタクより女性に与えるインパクトがもの凄く大きいということです。たとえ、女性にモテなくても莫大な印象を残す事ができる。その整数が持つインパクトの大きさをみることができるのが「絶対値」なのです。この絶対値はこれからも末永く使う概念ですのでシッカリ抑えておきましょう。

正の数・負の数のポイントは4つしかない

以上で中学数学の入り口「正の数・負の数」で理解すべきポイントでした。これから迫りくる中学数学モンスターたちに、今日学習したポイントを思い出して戦っていきましょう！

次回は、正の数・負の数を交えた四則演算についての記事を書いていきますね。

それでは！

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。