ひし形の対角線の求め方がわかる3ステップ

ひし形の対角線の求め方がわからない？？

こんにちは！この記事をかいているKenだよ。スパゲッティゆでまくったね。

ひし形の対角線の問題ってたまにでるよね？？

たとえばつぎのようなやつ↓↓

例題

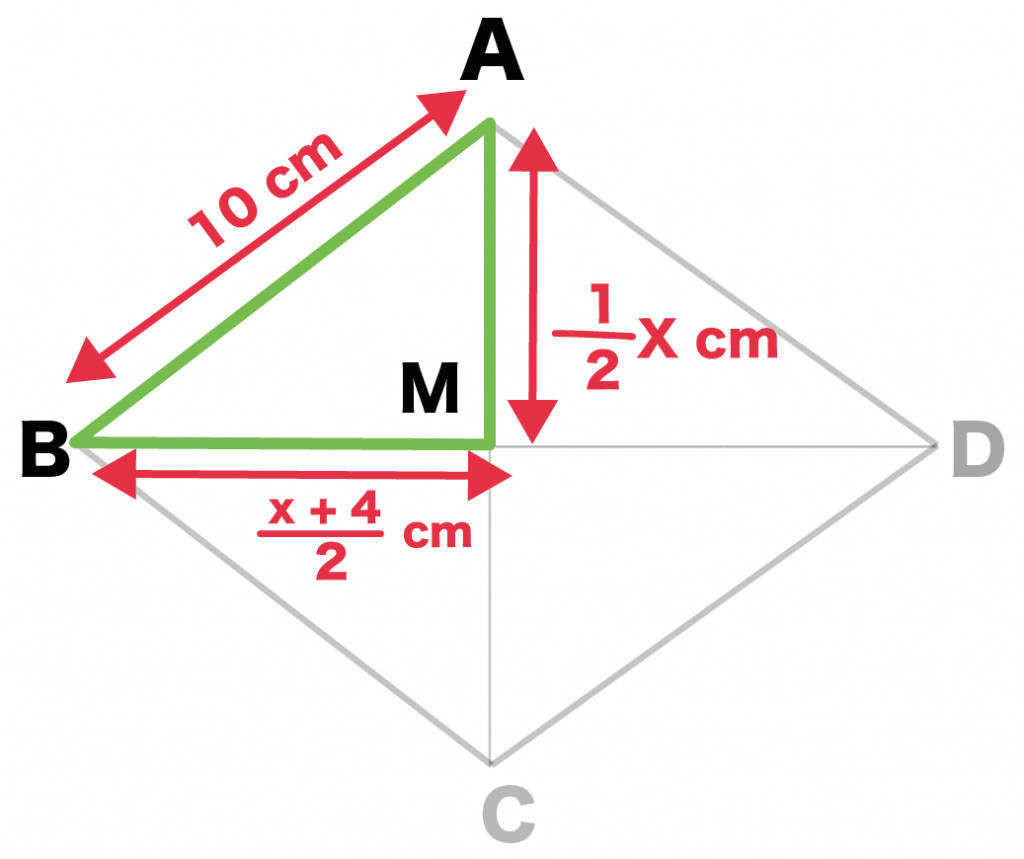
1辺の長さが10のひし形ABCDがある。2本の対角線のうち、一方は他方より4 cm長いとすると、対角線は何cmになりますか？？　※対角線の交点をMとする

この問題はぱっと見、むずかしい。

だけど、

うまーく問題をといてあげれば、

3ステップで答えをだせちゃうんだ。

今日は、

ひし形の対角線の求め方の3つのステップ

対角線をxとおく
対角線の半分をだす
三平方の定理をつかう

をわかりやすく解説してみたよ。

よかったら参考にしてみて^^

さっそく解説していくよ。

例題をといていこう！

例題

1辺の長さが10のひし形ABCDがある。2本の対角線のうち、BDはACより4 cm長いとすると、対角線ACは何cmになりますか？？　※対角線の交点をMとする

Step1. ある対角線の長さをxとする！

まず、対角線の長さを「x」とおこう。

例題では対角線ACをx cmとおいたよ。

対角線BDはACよりも4cm長いはずだから、

x + 4

になるね。

これが第1ステップ！！

Step2. 対角線の半分の長さを求める！

つぎは、

ひし形の対角線の「半分」を求めよう！

ひし形の定義で、

ひし形は平行四辺形である

ってならったよね？？

ってことは、ひし形でも平行四辺形の性質の、

対角線は中点で交わる

ってやつが使えるんだ。

ひし形ABCDでいうと、対角線ACとBDは中点Mでまじわっているはず。

ってことは、

MはACの中点だね。

計算してやると、

AM = 1/2 x

になる。

おなじように、

MがBDの中点でもあるから、

BM = (x+4)/2

になるね。

これが第2ステップ！！

Step3. 三平方の定理をつかう！

最後は、三平方の定理で方程式をつくろう。

対角線をひいてできた、

「小さな三角形」に注目するんだ。

ひし形ABCDでいうと、

三角形ABMだね。

ひし形の対角線の性質に、

垂直に交わる

があったね。

つまり、三角形ABMは角AMB= 90°の直角三角形なんだ。

こいつで三平方の定理をつかってやると、

10^2 = (1/2x)^2 + {(x+4)/2}^2

っていうxについての方程式ができるはずだ！

こいつを分数をふくむ方程式の解き方でといてやると、

x = 12

になるね。

つまり、

対角線ACは12[cm]ってことになる。

おめでとう！

ひし形の対角線の長さを求められたね！

まとめ：ひし形の対角線の求め方は三平方の定理でとどめ！

ひし形の対角線の求め方はちょっと複雑。

でも基本をおさえてしまえば、

っていう3つで対角線をもとめられるね。

どんどん問題になれていこう！

そんじゃねー

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。

ひし形の対角線の求め方がわかる3ステップ

ひし形の対角線の求め方がわからない？？