平行四辺形の面積の求め方の公式ってなに??
こんにちは!この記事をかいているKenだよ。みかん、最高。
平行四辺形の面積の求め方には「公式」がある。
1辺の長さをa、高さをhとすると、面積は、
ah
で計算できちゃうんだ。

つまり、
(平行四辺形の面積)= (平行四辺形の1辺)×(高さ)
ってわけ。
たとえば、1辺が10cm、高さが6cmの平行四辺形ABCDをイメージして。

こいつの面積は、
(平行四辺形の1辺)×(高さ)
= 10×6
= 60 [cm^2]
になるんだ。
どう??
むちゃ便利な公式でしょー?!
平行四辺形の面積の求め方がわかる3ステップ
でもでも、でもだよ?
なんでこの公式が使えるんだろう???
どうして平行四辺形の面積が「1辺×高さ」になるのか??
ちょっと気になる。。

そこで今日は、
平行四辺形の面積の求め方の公式
を3ステップで解説していくよ。
- 頂点から垂線を2本ひく
- 端の三角形を逆へ
- 長方形の面積を計算
よかったら参考にしてみて^^
Step1. 頂点から垂線を2本ひく
平行四辺形の頂点から垂線を2本ひこう。
向かいの辺に垂線をひけばいいんだ。
平行四辺形ABCDでは、
- 頂点AからBCへの垂線
- 頂点CからADへの垂線
の2本をひいてみたよ。

それぞれの交点をE、Fとしよう。
Step2. はしの三角形を逆側に!
はしっこの三角形を移動させよう。
三角形をナイフできりとって、
移動させるイメージね。
平行四辺形ABCDでいうと、
△CDFを、
逆の辺AB側に移動させるよ。

△CDFをナイフできりとって、

こいつを逆側の辺AB側に移動させてやる。

すると、
△ABEと△DCFは合同だから、
2つを組み合わせると、ぴたりとはまる。
んで、
新しいミニ長方形ができちゃうんだ。

Step3. 大きな長方形の面積を計算!
最後は、おーきな長方形の面積を計算すればいいんだ。

ミニ三角形を移動させてできた点をGとすると、
長方形GBCFの面積でいいんだ。
長方形の面積の求め方は、
タテ×ヨコ
だったよね??

ってことは、この長方形GBCFの面積は、
GB×BC
になるわけ。
BCは平行四辺形ABCDの「1辺の長さ」、
GBは「高さ」だね。
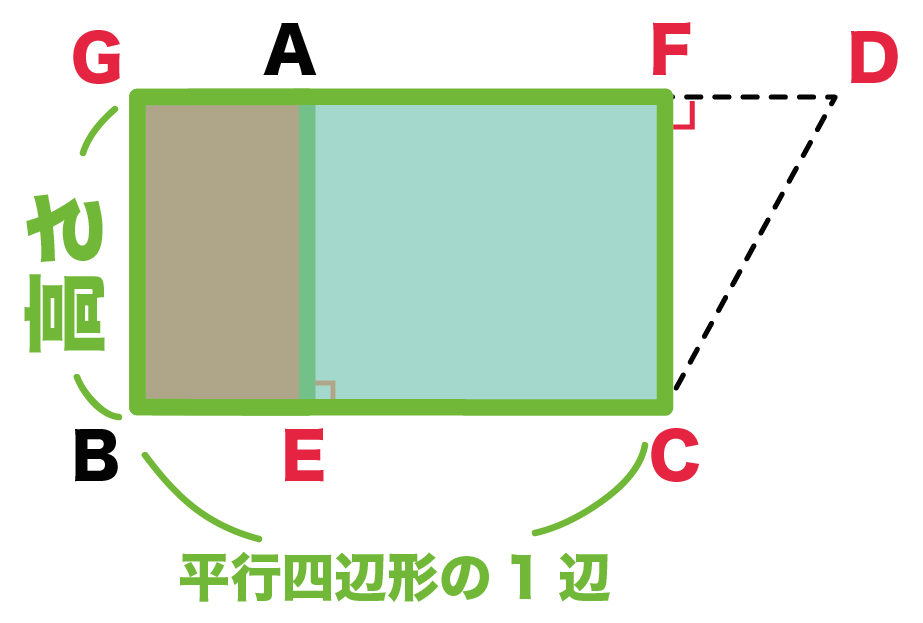
ってことは、
長方形GBCF
= 平行四辺形ABCD
= (1辺の長さ)×(高さ)
になるんだ。
おめでとう!
平行四辺形の面積の公式をゲットしたね!
まとめ:平行四辺形の面積の求め方は三角形を切り取ろう!
平行四辺形の面積の求め方??
そんなの簡単さ。
三角形をナイフできりとろう。
あとは、そいつを逆サイドに移動させるだけ。
1辺×高さ
の公式をじゃんじゃん使っていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






質問する