3分でゲット？？八角形の内角の和がわかる公式

八角形の内角の和の公式ってあるの？？

こんにちは！この記事をかいているKenだよ。ほっけ、焼いたね。

八角形の内角の和って気になるよね？？

8角形・・・

みてるだけで内角の和を求めたくなる。

うん、わかるよ、その気持ち。

今日はそんなときのために、

八角形の内角の和の求め方を紹介していくよ。

よかったら参考にしてみてね^^

八角形の内角の和を3秒で計算できる公式

8角形の内角の和はチョー簡単。

もうね、一瞬だよ一瞬。

多角形の内角の和の公式をつかっちゃえばね^^

念のために復習しよう。

n角形の内角の和を求める公式は、

180°×（n-2）

だったよね？？

八角形の内角の和を求めたいときは、

「n」に「8」をぶちこんでやればいいんだ。

すると、

180°×（n-2）
= 180°×（8-2）
= 180×6
= 1080°

になる！

つまり、八角形の内側の角をぜーんぶたしてやると、

1080°になるってことさ。

8角形の内角をa~hとしてやると、

a + b + c + d + e + f + g + h = 1080°

になるんだ。

なんで内角の和が1080°になるの？？

でもでも、

なんで多角形の内角の和の公式が使えちゃうんだろう？？

便利すぎてバチあたらねえかな・・・

って心配しはじめるはずだ。

その理由はずばり、

八角形の中に三角形が6個かくれているから

なんだ。

こんな感じで八角形に対角線をひいてみると、

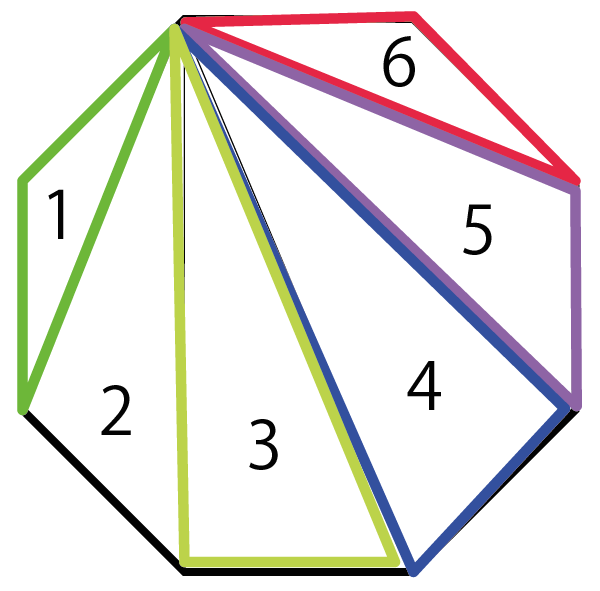
1、2、3……6個の三角形をみつけられるはず。

そんで、

1つの三角形の内角の和は「180°」だったね？？

ってことは、

三角形が6個もふくまれている八角形の内角の和は、

180°を6倍して「1080°」になるってことさ。

まとめ：八角形には三角形が6個もかくれている！

八角形の内角の和をもとめたいときは、

180°（n-2）

という公式のnに「8」をいれちゃえばO.K。

計算すると1080°になるから、

8角形の内角の和は？？

って問いつめられたらドヤ顔で

1080°ですが？なにか？

答えてやろう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。