【数の大小】数直線を使いこなす3つメリット

数直線を使いこなさないと損？？

こんにちは！みなさん、数直線をしっかり使いこなしていますか？？

数直線は、正の数・負の数の単元で登場する数学の道具です。はじめて「数直線」という言葉を耳にした方のためにブリタニカ国際百科事典で調べてみると、

実数を表わす直線。1つの直線 l を考え，l 上に1点Oをとり，0と対応させて E₀ とし，また長さの単位を定めて，E₀ から単位の長さだけ進んだところを E₁ とし，線分 E₀E₁ に数1を対応させる。

だそうです。ちょっとわかりにくいのでシンプルにしてあげると、

数字を表現できる直線（一部をのぞくよ）

というわけですね。1000も-90もなんだって1つの直線で表すことができるのです。よくよく考えてみると、数直線ってスゴいですね笑

数直線の基本的な2つのルール

それでは数直線を使いこなしてみましょう！

数直線には以下のような3つのルールが存在しています。

1. 数直線は「直線」である

数直線はかならず「直線」でないといけません。曲線を含んでいたり、

凹凸があってはいけません。

数直線にアクセントをつけたい気持ちはわかります。がしかし、ここはいたずら心をぐっと抑えて「直線」をひくようにしましょう。

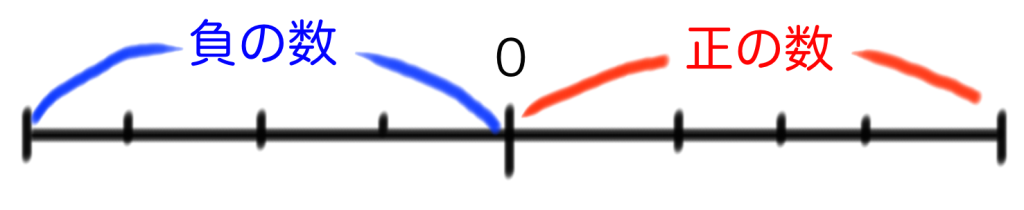
2. 原点より左を「負の数」、右を「正の数」

つぎに、数直線のうちのどちらのサイドを「負の数側」、「正の数側」にするのかを決定します。さもなくば、それぞれがオリジナルの数直線を使いだします。

みんなちがって、みんないい

と詩人の金子みすずはかつていいましたが、数直線の場合は「みんな一緒」にしましょう笑

ルールは簡単。原点（０）よりも左の直線側を「負の数（−）」とし、逆に右の直線側を「正の数（＋）」とするだけです！！

数直線を使いこなすと起こる3つのキセキ

それじゃあ、いったい全体、数直線という数学のアイテムを使って何がお得なのでしょうか？？　お金がもらえる？　モテる？　お腹がいっぱいになる！？

いやいや。じつは冷静になってみると、以下の3つのメリットが数直線にはあることを気づかされます。

1. 絶対値を理解しやすい

ひとつめの数直線のメリットは、

絶対値を理解しやすい

ということです。絶対値とは「絶対値の意味を5秒で理解できる方法」という記事でお伝えしたとおり、

ある数字の原点（ゼロ）からの距離

でしたね。一見、わかりにくい絶対値の概念です。だがしかし、数直線という数学のアイテムを駆使してやると、急にわかりやすくなっちゃうんです。

たとえば、-9の絶対値。「ねえねえ、-9の絶対値って何なのよ？　教えないとぶつわよ？」と美女に迫られても即答できません。これは肉体的な痛みを伴いますし、おおいにチャンスを逃しています。

そこで登場するのが「数直線」。直線を書いて、原点（ゼロ）をとって、ゼロより左側に9ついったところに「-9」をプロットします。

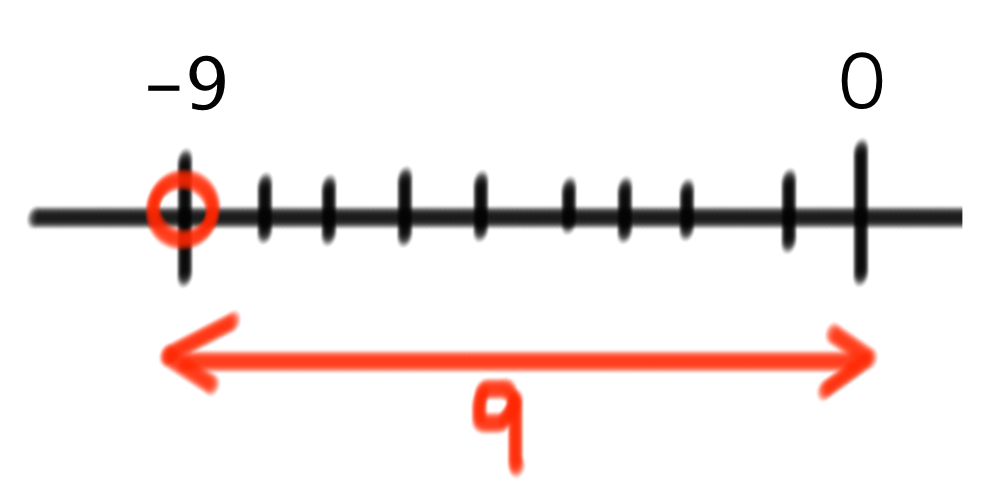
すると、この数直線を眺めているだけで「-9」の絶対値を察することができます。なぜなら、-9が0より9つ左に離れていることがわかるからです。

数直線を使えば「絶対値の意味」を視覚的に理解できるわけですね！あー便利便利！

2. 数の大小を直感的に理解できる

ふたつめのメリットは「数の大小」です。2つの数字を数直線上にプロットする。これだけで2つの数の大小関係を3秒、い、いや、1秒ぐらいで理解することができます。

たとえば、「-0.5と-0.3のどちらが大きい数字ですか？？」と問われたとしましょう。こんなときは、頭の中だけで考えるのでなく、実際に数直線上に2つの数字を書き出してみればいいのです。こんな感じで↓↓

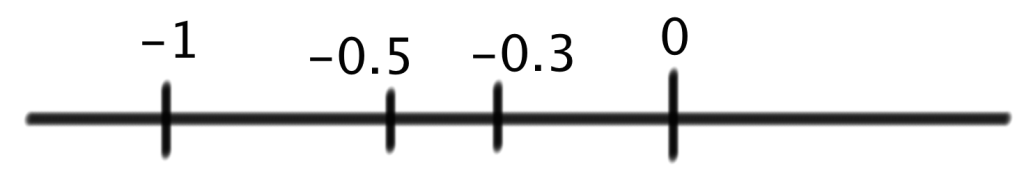
すると、「-0.3」のほうが「-0.5」より右にあるため、「-0.3」のほうが大きい数である、ということがわかります。数の大小の問題がテストに出たときは迷わずに数直線上に書き出してみましょう。

3. 正の数・負の数の計算が楽になる

最後は「正の数と負の数が混じった計算」を楽におこなうことができる点です。

＋と−の符号が入り交じった計算は馴れるまでに時間がかかります。まず2つの数の絶対値の大小を比較して、こっちがでかいからあっちをひいて・・・などなど。これではひとつの数学の問題に時間をかけすぎてタイムアップになってしまいます。

そこで登場するのが、数直線というヒーローなのです。実際の例題で確認してみましょう。-9+2という計算問題があったとします。これを実際にといてみると、

1. 「-9の絶対値が2のそれより大きい」
2. 9と2の差は7
3. 絶対値の大きい-9は負の数
4. 答えも負の数。
5. こたえは-7

という計算過程を踏まねばなりません。一見シンプルな計算にみえますが、思考の過程を書き出してみると複雑であることがわかります。

それでは、この計算に数直線を使ってやるとどうなるでしょうか？？

まず-9を数直線上にプロットします。

これに2と足すということは、数直線上を右に2つすすむことを意味します。よって、-9にプロットされていた点は、

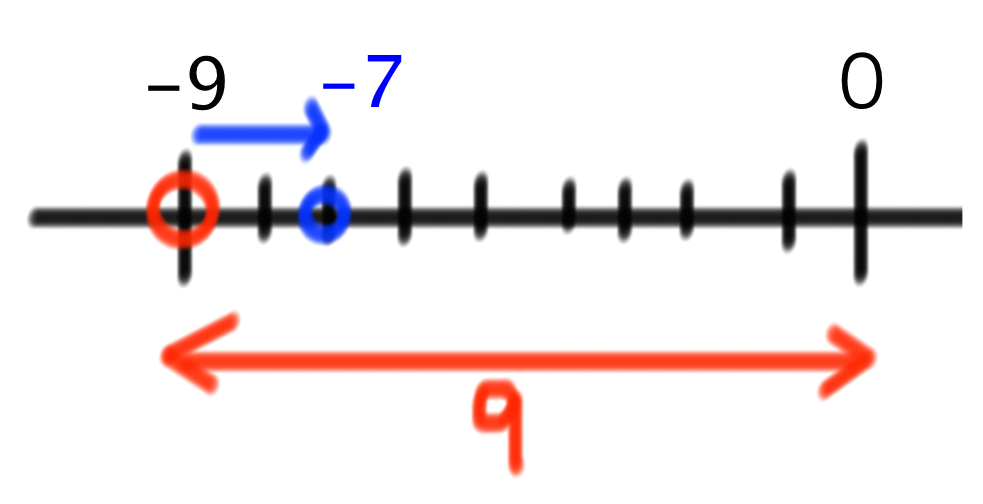
-7の点に移動します。つまり、この計算の答えは「-7」ということができます。

以上のように、数直線をつかえば「正の数と負の数の計算」を視覚的に、より直感的に理解できます。しかも、うっかり計算ミスをも防ぐ効果もあります。

テストで時間があまったときは数直線で答えを見直してみましょう！！

数直線をつかうとベンリ！！

数直線が便利な3つの理由を紹介してみました。いかがだってでしょうか？？

ぼくは中学生の頃、数直線を馬鹿にしていました。

こんなのただの直線だ！　子供だましだ！

なんて具合にです笑　ただ、大人になってみて中学数学を復習してみて、

数直線は数字・計算を視覚的に理解できるツールである

ということがわかりました。数直線に惚れ直したというわけです。

これから中学の数学を勉強する読者の方は未来があります。せっかく中学校で「数直線」を学習しますので、積極的に利用してみてくださいね！

それでは、また今度です。

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。