中学数学で「指数の計算」には気をつけろ!!
中学校で勉強する数学には「指数の計算」が山のように出没します。
もうその指数の数は多すぎて数えられないほど。中学校の数学が指数で成り立っているといっても過言ではありません。

ところが、です。
中学数学で登場する「指数の計算」にはたくさんの落とし穴が潜んでいます。
はあ?指数の計算!?ラクショーだよそんなの
となめてかかるとゼッタイに痛い目に合います。中間・期末テストでとれたはずの点数が指数計算のケアレスミスによって台無しに。それじゃあモッタイナイですよね??
そこで今日は、
中学数学の「指数の計算」で注意すべき3つのポイント
をお伝えします。指数の計算が苦手な中学生の方や、これから指数を勉強する数学初心者の方までが参考にしてくださるとうれしいです。
中学数学の「指数計算」で気をつけたい3つのポイント
それじゃあさっそく、指数計算で注意すべき点を3つ紹介していきます。ポイントをしっかり押さえて数学テストでのケアレスミスを少なくしましょう。
1. 指数とカッコの位置
指数の計算で多くの人が陥りやすい落とし穴は「指数と()」の位置関係の誤解です。これは負の数の指数計算で間違える方が多発するケース。えっ、いったいどんな指数計算の落とし穴なのかですって??
それは、
負の数の()の外に指数があるか、内に指数があるか計算結果が異なる
ということです。()の外に指数があると、負の数自体を繰り返し掛けていることを意味します。逆に、()の内に指数があると指数がついた数字(低)を繰り返しかけた数に「マイナス記号」をつけていることになります。
ちょっと言葉では言い表しづらいので、実例をもとに確認していきましょう。
たとえば、という指数の計算があったとします。これを計算しないと給食が食えません。
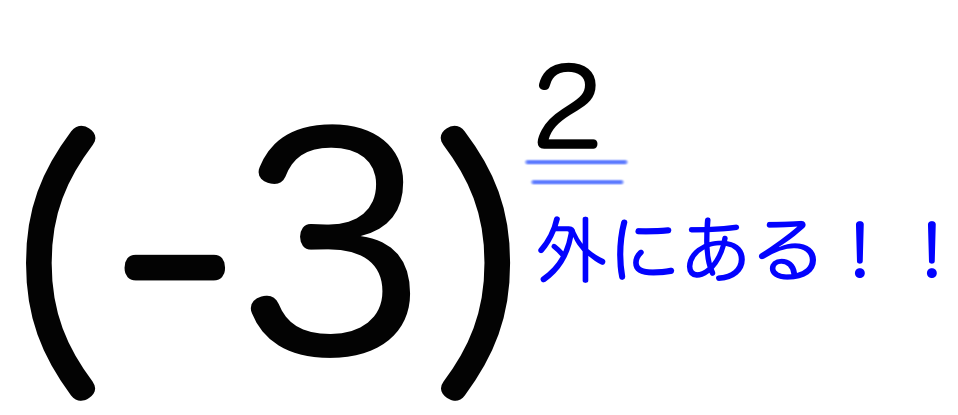
このケースは「()の外側に指数がある」場合です。つまり、(-3)という負の数自体を2回繰り返し掛け合わせた数なので答えは、となります。
それではという指数の計算はどうなるでしょうか??
これは先ほどのと異なり、2という指数が()の内側に入っていることがわかります。

そのため、この計算は「3を2回繰り返しかけた数にマイナスの符号をつける」ことを意味します。よって、指数計算の結果は、
以上の2つの指数計算はかなり似ています。もうリリとララぐらい似ています。だって、指数の位置が()の「内」か「外」だけの違いですからね。
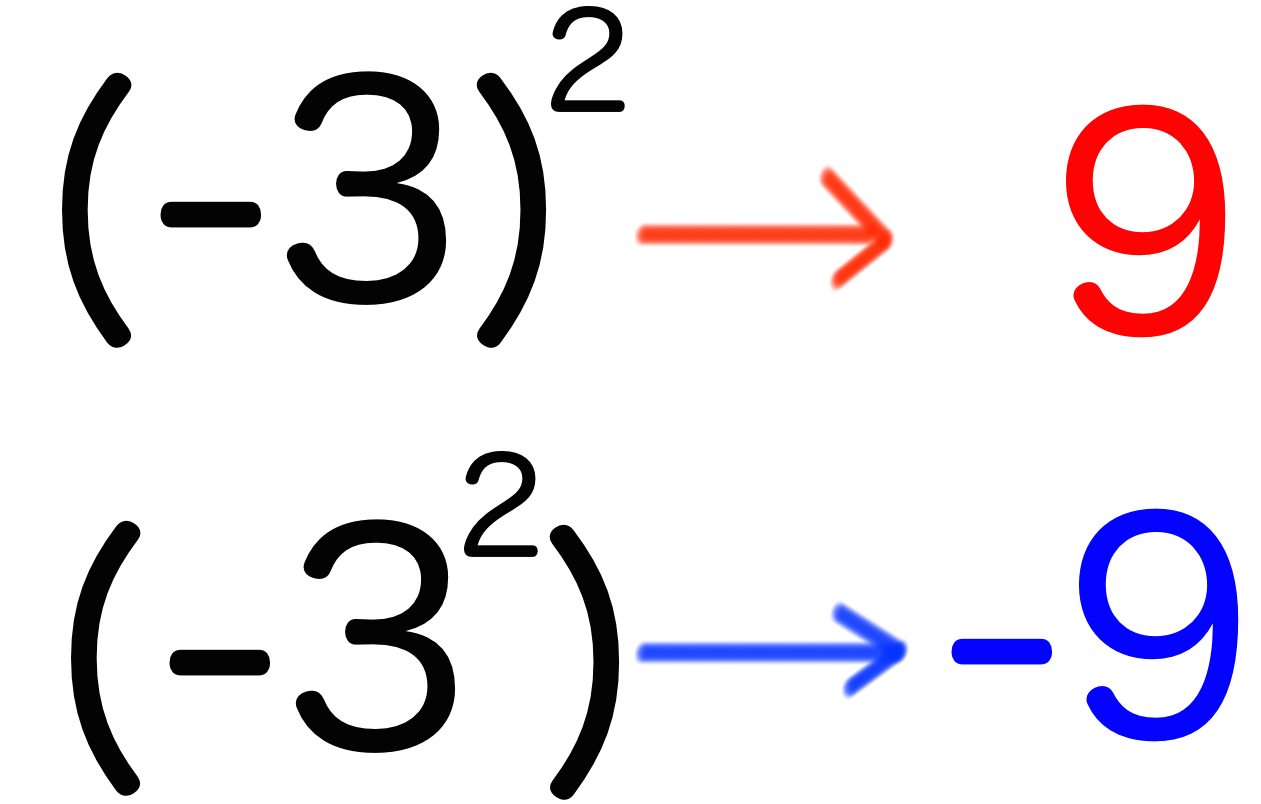
負の数の計算で「()と指数の位置」が異なると「計算結果の符号」が異なることを肝に命じておきましょう。
2. 指数が偶数か?奇数か??
2つ目に気をつけるべきことは「指数の数」です。
えっ。指数の数に気をつけるのは当たり前ですって??た、たしかに。指数は「同じ数を繰り返しかけあわせる数」です。注意しないわけにもいきません。
ぼくがここで言いたかったのは、
(負の数の指数計算の場合に)指数が「奇数か偶数か」に注意して計算する
ということです。ここで言う「負の数」とは先ほど解説した()の外側に指数が置いてあるケースです。たとえばといった計算ですね。このとき、
- 指数が奇数→こたえが負の数
- 指数が偶数→こたえが正の数
となります。説明だけではちょいとわかりづらいので具体例をみていきましょう。
たとえば、と
の計算を例にとります。両者ともカッコの外側に指数がありますね??この指数の計算は「-3を繰り返し掛け合わせる」ということを意味します。
よって、2つの指数の計算結果は、
となります。
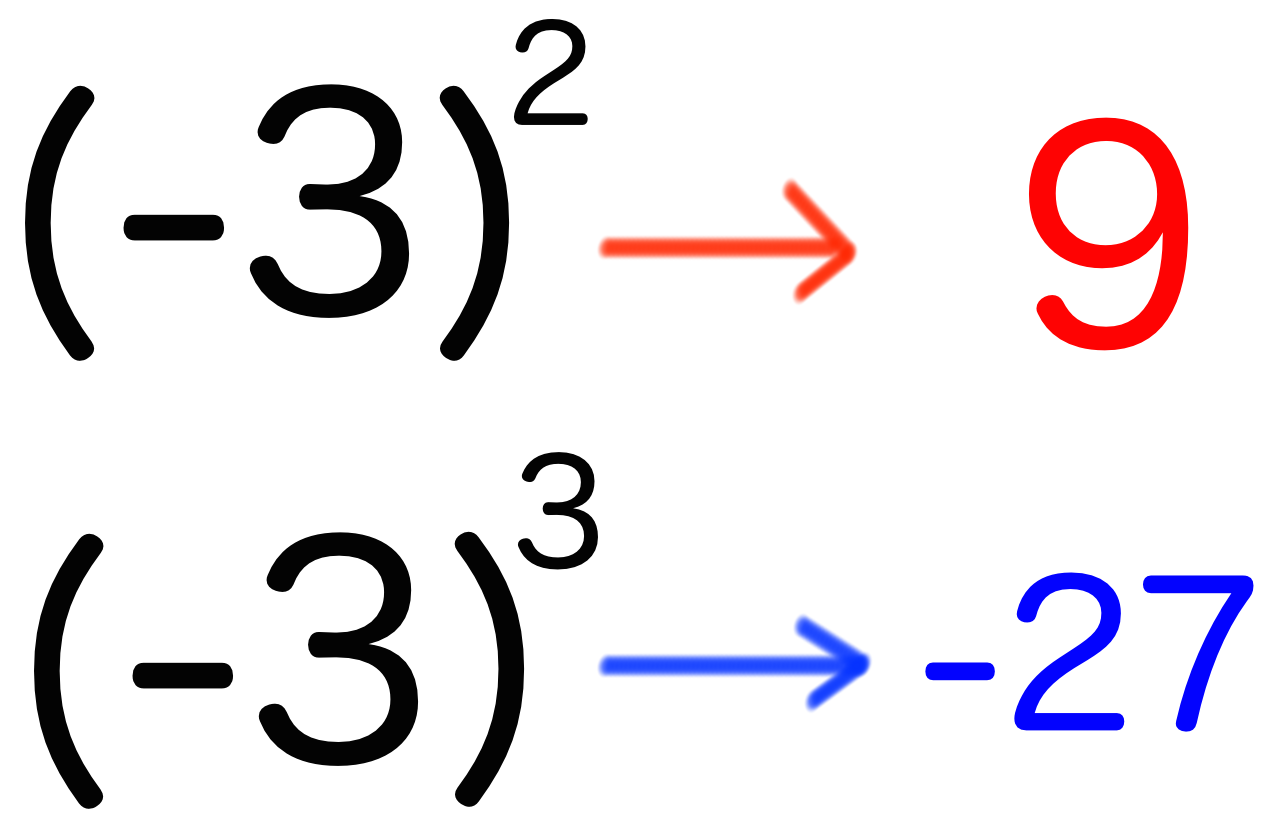
この指数の計算例をみても、
- 指数が偶数→こたえは正の数
- 指数が奇数→こたえは負の数
となっていることがわかります。ただ、このれは「()の外側に指数があるときのみ」有効になります。指数の計算をする前にはよーーく目をこすっておきましょう。
3. 「0以上1未満の数」の指数計算
最後に指数の計算で注意すること。それは
絶対値が1より小さく0より大きい数(0<a<1)の指数計算
です。1よりも小さい数とはたとえば、や
などのことですね。こんな数字に指数がついてしまったケース、
や
のときに注意すればいいのです。
ここで覚えて欲しいことは一点だけ。
「1より小さく0より大きい数字」の指数計算をすると、もとの数より小さくなる
ということです。
く、繰り返し同じ数を掛けたんだから大きくなるはず!!
といいたい気持ちは十分にわかります。ただ、「絶対値が1より小さく0より大きい数」にだけは気をつけておきましょう。
たとえば次のような指数の問題があったとします。
つぎの数の大小を比較しなさい。間違えたらビンタします。
と
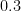
このとき「2乗したほうが大きくなるはずやろ??」という固定概念をもっていると、
と思わず答えてしまいそうです。これだと手痛いビンタを頬に食らうことになります。
ここは冷静沈着になって試しに指数の計算をしてみましょう。すると、
となります。これは明からに元の数「0.3」より小さいですよね???
よって答えは「」となります。2乗や3乗しても必ずしも元の数より大きくならないことに気をつけましょう!
指数の計算で注意すべくは3つのポイントのみ!!
以上で指数の計算で気をつけるポイントは終了です。
たった3つのことを頭にいれておくだけで、指数の計算のケアレスミスを避けることができるのです。中学数学では指数の計算が死ぬほど登場します。指数という言葉で耳鳴りがするほど。
そんだけ頻繁に登場する指数の計算でミスをなくせば、数学テストの点数がグングンと昇っていくでしょう。
それでは、また今度です。
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







カッコがついてない時の見分け方を教えてください。
カッコがついてない時は、符号は一旦無視して、まずは指数を計算。
後から符号をつければいいね
指数を含む計算の掛け算はどうやればいいですか?
例 (-4)2×(-0.52)
お願いします!
> (-4)2×(-0.52)
指数をふくむ計算のときは、まずは指数を計算して、
それから掛け算をするといいよ
カッコがついてない時の計算のやり方をもっとわかりやすく教えて欲しいです…
>カッコがついてない時の計算のやり方をもっとわかりやすく教えて欲しいです…
()がついてない時は()の内側に指数がある場合と同じだね。
数字についている符号は一旦無視して指数の計算だけやろう
どうすれば、数学が楽しくなりますか?
>どうすれば、数学が楽しくなりますか?
問題が解けること、日常でどのように数学が活かされているかを知る、数学を勉強して身につくスキルを認識する
などがあるかな!
まずは基礎を抑えて少しずつ問題を解いていこう!
16a²-4a²=12a²であってますか?
>16a²-4a²=12a²であってますか?
そうだね!
(-2x二乗y二乗)3乗
>(-2x二乗y二乗)3乗
数字と文字で別々に累乗して最後に合わせると計算しやすいかも!
まずは-2の3乗から!
かっこの中に足し算や引き算がある時はどうすれば良いですか?
例(〇+〇)2
このような場合は先にかっこの中で計算するんですか?
曖昧なので教えて頂きたいです!
大きい指数がある場合はどうすれば簡単に解くことが出来ますか?