【簡単公式】円柱の表面積の求め方がわかる3ステップ

「円柱の表面積の求め方」の公式ってあるの？？

こんにちは、この記事をかいているKenだよ。やっぱ土日はすばらしいね。

円柱の表面積を3秒ぐらいで計算したい。

そんなときは、

円柱の表面積の求め方の公式をつかってしまえば2秒ぐらいで計算できちゃうんだ。

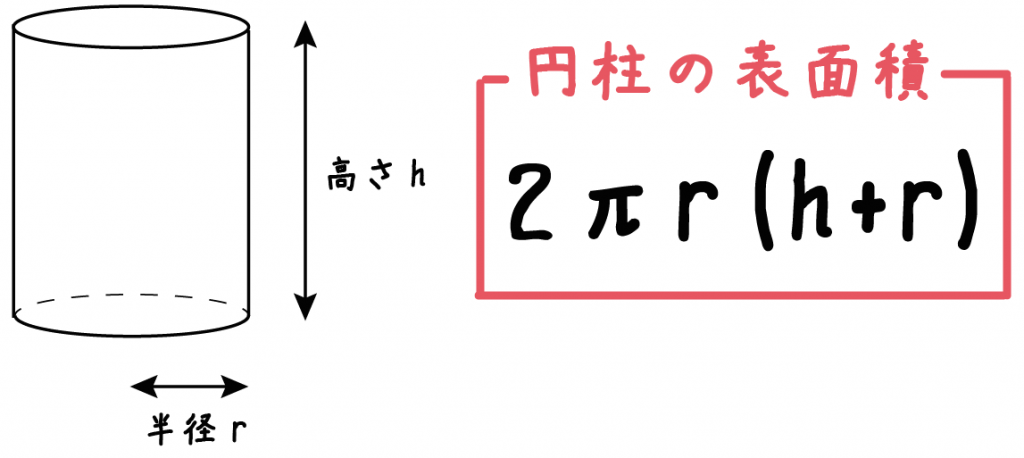
下の図のように、円柱底面の半径をr、高さをhとすると、

2πr(h+r)

で求めることができるよ^^

つまり、

2×円周率×半径×（高さ+半径）

ってわけだね。

公式はむちゃくちゃ便利だけど、テストで忘れちゃうかもしれないよね？？

そういうときのために今日は、

円柱の表面積の求め方を3ステップで解説していくよ。

3ステップでわかる！円柱の表面積の求め方

例題をときながら円柱の表面積の求め方を勉強していこう。

例題

半径3cm、高さ10cmの円柱の表面積を求めなさい。

つぎの3ステップで求めることができるんだ。

Step1. 底面の面積を求める！

円柱の底面積をもとめてみよう。

円柱の底面は「円」。

よって、底面積の求め方は、

半径×半径×円周率

になるよね！？？

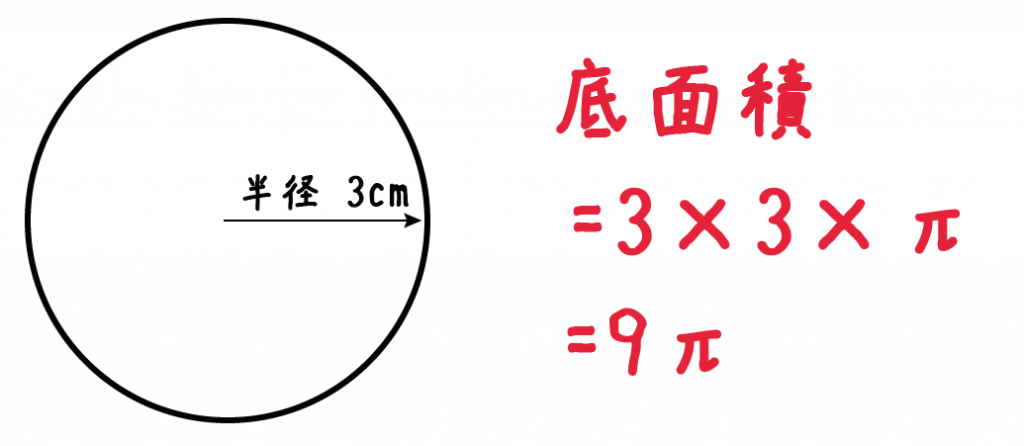
ってことで、例題の円柱の表面積は、

3×3×π = 9π

になるね！

Step2. 円柱の側面積を計算する！

つぎは円柱の側面積を計算しちゃおう！

円柱の側面積は、

（底面の円周長さ）×（円柱高さ）

で求められるだったよね？？

底面の円周長さは6πになるよね。ってことは、例題の円柱の側面積は、

6π×10= 60π

になる。

Step3. 「底面積」を2つと「側面積」を1つをたす！！

円柱の展開図をイメージしてみると、

「底面が2つ」＋「側面が1つ」

になっていることがわかるよね？？　だから、円柱の表面積は、

（底面積）×2 + 側面積

で求められるってこと！

さっそく、例題の表面積を求めてみよう。

底面が2つ、側面が1つだから、

9π×2　+  60π

= 78π

になるね！

おめでとう！円柱の表面積の問題を瞬殺できるようになったね！！

まとめ：「円柱の表面積の求め方」は公式なんかいらねえ！

円柱の表面積は公式を使えば2秒で計算できる。

だけれども、公式に頼らなくたって、5分ぐらいで計算できちゃうよね笑

ってことで、公式に頼らない求め方もおぼえておこう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。