1次関数の直線の式の求め方がわからない??
こんにちは!この記事をかいているKenだよ。洗濯物ためすぎたね。
一次関数の式を求める問題
ってけっこうあるよね。下手したら、3問に1問ぐらいは出るかもしれない。
テスト前におさえておきたい問題だね。

今日はこの「直線の式を求める問題」をわかりやすく解説していくよ。
よかったら参考にしてみてね^-^
一次関数の直線の式がわかる3つの求め方
まず、直線の式が計算できるケースを確認しよう。
つぎの4つの要素のうち、2つの値がわかっているときに式が求められるんだ。
- 傾き(変化の割合)
- 切片
- 直線が通る座標1
- 直線が通る座標2
たとえば、傾きと切片がわかっているとき、とか、座標と切片がわかっているとき、みたいな感じだね^^

求め方のパターンをみていこう!
パターン1. 「傾き」と「切片」がわかっている場合
まずは一次関数の「傾き」と「切片」の値がわかっている場合だ。
たとえば、つぎのような問題だね。
例題
yはxの一次関数で、そのグフラの傾きは-5、切片は7であるとき、この一次関数の式を求めなさい。
このタイプの問題はチョー簡単。
一次関数の式「y = ax + b」に傾き「a」と切片「b」の値を代入するだけだよ。
例題での「傾き」と「切片」は、
- 傾き: -5
- 切片:7
だね。
だから、一次関数の直線の式は、
y = -5x + 7
になる。
代入すればいいだけだから簡単だね^^
パターン2. 「傾き」と「座標」がわかってる場合
つぎは「傾き」と「座標」がわかっている場合だ。
たとえばつぎのような問題だね。
例題
yはxの一次関数で、そのグラフが点(2, 10)を通り、傾き3の直線であるとき、この一次関数の式を求めなさい。

この手の問題も同じだよ。
一次関数の式「y = ax + b」に傾きaと、座標を代入してやればいいんだ。
bの方程式ができるから、そいつを根性でとくだけさ。
例題では、
- 傾き:3
- 座標(2, 10)
っていう一次関数だったよね??
まずはaに傾き「3」を代入してみると、
y = 3x +b
になるでしょ? そんで、こいつにx座標「2」とy座標「10」をいれてやればいいのさ。
すると、
10 = 3 × 2 + b
b = 4
になるね。
つまり、この一次関数の式は「y = 3x + 4」になるよ!
こんな感じで、傾きと座標をじゃんじゃん代入していこう!^^
パターン3. 「切片」と「座標」がわかっている場合
つぎは「切片」と「座標」がわかっている問題だね。

たとえば、つぎみたいなヤツさ↓↓
例題
yはxの一次関数で、そのグラフが点(2, 11)を通り、切片3の直線であるとき、この一次関数の式を求めなさい。

このタイプの問題もいっしょ。
一次関数の式「y = ax +b」に切片と座標を代入してやればいいんだ。
そんで、できた方程式を解いてやれば直線の式が求められるね。
例題では、
- 切片:3
- 座標(2, 11)
だったね?
切片の「3」をy = ax+bに代入してみると、
y = ax + 3
になるね。
そんでコイツに、
- x座標「2」
- y座標「11」
を代入してやると、
11 = 2a + 3
になる。
この方程式をaについて解いてやると、
11 = 2a + 3
2a = 8
a = 4
になる。
つまり、この一次関数の傾きは「4」ってことだ。
だから、
一次関数の式は「y = 4x + 3」になるね。
このタイプの問題も代入して方程式をとくだけさ!
パターン4. 直線を通る2点がわかっている場合
最後は、直線が通る2点の座標がわかっている問題だ。
たとえば、つぎのような問題さ。
例題
つぎの一次関数の式を求めなさい。
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
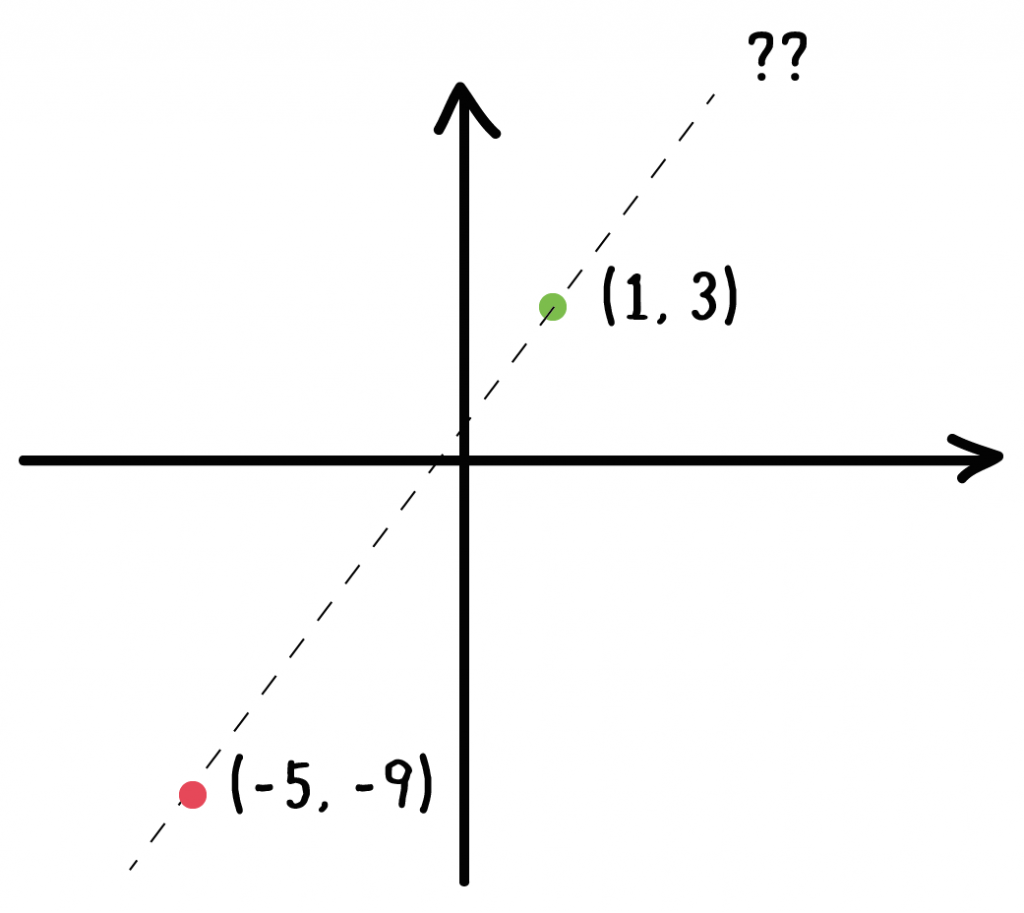
ちょっとめんどくなるけど、解き方はこれまでと一緒。
一次関数の式「y = ax + b」に2点の「x座標・y座標」を代入してやればいいのさ。
問題に慣れるまで練習してみてね^^
まとめ:直線の式を求める問題は4パターンで攻略できる!
直線の式を求め方はどうだった??
4パターンあるとか言っちゃったけど、
だいたいどれも解き方は一緒。
一次関数の式「y = ax + b 」に、
- 傾き
- 切片
- 座標
のうち2つを代入してやればいいんだ。
テスト前によーく復習してね^^
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。




























『点(2.1)を通り、直線y=2x+1に平行な直線の式を求めなさい』という問題の解き方に悩んでいます。教えてください!
y=2x+1に平行な直線ってことはこの直線の傾きはいくつかな?
y=3分の2x+2に平行な直線の式でy=3分の2x+bまでは分かりました、bの求め方が分かりません
平行な直線ってことから、変化の割合がわかったら、あとはその直線が通る座標(x、y)を代入するだけ!
y=3分の2x+b
に、通る座標のxとyを入れてbを出してみよう
xの値が4増加するとyの値は12増加し、
(0,-2/7)を通る直接の求め方が分かりません
わかりやすく教えてくれると有難いです
まずはxとyの増加量から変化の割合を計算しよう。
変化の割合はy=ax+bのaのことだから、あとは、この式に座標を代入してbを求めるんだ!
y=ax+3
もうひとつヒント欲しい!
一次関数y=−二分の三+6のグラフとx軸との交点の座標を求めよ。と言う問題がわかりません。
どうやったら良いのでしょうか?
x軸との交点ってことはy座標が0ってこと!
y=0を代入してその時のxを求めよう
(-3,0)と(-3,6)を通る直線の式が分かりません。
二点の座標
直線の式を求める問題で、二点(0.1)(1.5)を通る直線の求め方がわかりません。
教えてください
直線の式を求めたいのですが、その直線の座標(0,-2)と、(0,6)と(4,0)の直線があります。その2つの直線の交点がx座標とy座標がともに自然数の値をとる時の直線の式をもとめられますか?(0,6)と(4.0)の直線の式は求められたのですがそれからわかりません。
一番簡単なのは連立方程式を使う方法かな。
y=ax+bに2つの座標を代入して連立方程式を作ってみよう
連立方程式を使ったやり方がわかりやすいよ!
y=ax+bに2つの座標を代入して連立方程式を作ればいいんだ
座標(0,-2)を通る直線をy=ax-2としてみよう。
そして、(0,6)と(4.0)の直線の式との交点をaで表してみて
質問してもいいですか ??
基本的な( ? )問題がわからないです
( 1 )
yはxに比例し、x=3のとき、y=6である。このときのyをxの式で表しなさい。
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
( 2 )
yはxに反比例し、x=8のときy=-3/4である。xとyの関係を式に表しなさい。
>yはxに比例し、x=3のとき、y=6である。このときのyをxの式で表しなさい。
比例定数はy÷xで計算できるね。
比例定数はy=axのaのこと
>yはxに反比例し、x=8のときy=-3/4である。xとyの関係を式に表しなさい。
反比例の場合、xyで比例定数を計算できるね。
y=x分のaのaが比例定数だ
Xの増加量が2の時、yの増加量が-3/2で、点(-4,10)を通る直線を求めるっていう問題が分かりません。
>Xの増加量が2の時、yの増加量が-3/2
まずはこの情報から変化の割合を計算してみて。
変化の割合はy=ax+bのaのことだから、あとはbを求めるために座標を代入しよう
ごめんなさい汗
学校の宿題です。
〈yはxの一次関数である。xの増加量が3のときのyの増加量は2であり、そのグラフは点(3,-1)を通る。この一次関数の式を求めよ。〉
これが全く分かりません汗
よろしくお願いします
>yはxの一次関数である。xの増加量が3のときのyの増加量は2であり、そのグラフは点(3,-1)を通る。この一次関数の式を求めよ。
まずはxの増加量とyの増加量から変化の割合を計算しよう。
変化の割合はy=ax+bのaのことだから、あとはその式に通る座標を代入してbを出せばオッケー
学校からの宿題で、反比例のグラフから傾きと切片を求めなければいけません❗
でも、求め方が分かりません よろしくお願いします‼
>学校からの宿題で、反比例のグラフから傾きと切片を求めなければいけません❗
でも、求め方が分かりません よろしくお願いします‼
比例のグラフのことかな?
傾きは比例定数、切片は0だよ!
反比例には傾きと切片はないね〜
y=3x+7 のグラフとy軸について対称な直線を求めなさい という問題がよく分かりません。 教えて頂けたら幸いです。 宜しくお願い致します。
>y=3x+7 のグラフとy軸について対称な直線を求めなさい
よくわからないときはまずは図をかいてみるといいよ。
y軸に対称ってことは、切片は変わらずに、傾きにマイナスがつくよ
点A(0,7) を通り、直線M(y=3分の2x+2)に平行な直線の式を求めなさい
という問題が分かりません泣
こんなバカな私にも分かりやすいように教えて下さるとありがたいです!
グラフが点(-8,12)を通り、y=-4分の3のグラフに平行な直線である。… これってどうやって解くのですか?
>点A(0,7) を通り、直線M(y=3分の2x+2)に平行な直線の式を求めなさい
ヒントは平行ってことだ。
ある直線に平行だと、その関数と「傾きが一緒」なんだ。
だから、直線Mの傾きの3分の2と同じってことね。
y=ax+bのaが3分の2ってことだからあとはbを求めるだけ。
点Aの座標を代入してbを求めてみよう
>グラフが点(-8,12)を通り、y=-4分の3のグラフに平行な直線である
平行ってことは傾きが等しいってこと。
y=-4分の3はx軸に平行な直線だから、傾きは0になるよ。
グラフを実際に書いてみるとわかりやすいかも。
x軸の正の向きに3進むとY軸の正の向きに2進み点(6,-1)を通る直線
の求め方が分からないです
切片が分数のときって、どうやってグラフを書いたらいいですか?
>x軸の正の向きに3進むとY軸の正の向きに2進み点(6,-1)を通る直線
の求め方が分からないです
xが3進むとyが2進むってことから変化の割合、つまり傾きを計算しよう。
傾きはy=ax+bのaのことだから、あとは(6,1)を代入してbを求めるだけ
>切片が分数のときって、どうやってグラフを書いたらいいですか?
xとyの座標が両方整数になる2点を結んであげよう
グラフの傾きが-2で、点1,2を通る直線が分かりません
>グラフの傾きが-2で、点1,2を通る直線が分かりません
傾きが-2ということはy=ax+bのaが-2。
で、y=-2x+bに点1,2を代入してbを求めてみよう!
X=-4のときy=0、x=2のときy=3となる一次関数がある。この関数においてx=5の時のyの値を求めよ。 という問題の解き方を教えてください
>X=-4のときy=0、x=2のときy=3となる一次関数がある。
この関数においてx=5の時のyの値を求めよ。 という問題の解き方を教えてください
「X=-4のときy=0、x=2のときy=3となる一次関数がある」という情報から、連立方程式を作って一次関数の式を求めてみよう。
式がもとまったらx=5を代入してyをゲットしよう
X=2のときY=-4で、Xの増加量が3のときのyの増加量が-3の直線
と言う問題の解き方を教えてください。
>X=2のときY=-4で、Xの増加量が3のときのyの増加量が-3の直線
xとyの増加量から変化の割合を計算しよう。
一次関数の変化の割合は傾きのことだから、y=ax+bのaがわかるね。
あとはその式にxとyを代入してbを求めよう
質問してもいいですか?
y軸に平行で(5.-2)を通る直線
の求め方がよく分からないです。
>質問してもいいですか?
y軸に平行で(5.-2)を通る直線
の求め方がよく分からないです。
y軸に平行ってことは、xの値がずーっと一定の関数ってこと!
グラフを実際にかいてみるとわかりやすいね
変化の割合が4でX=5のときy=13の一時関数がわからないです
>変化の割合が4でX=5のときy=13の一時関数がわからないです
一次関数の変化の割合は傾きのこと。
この例でいうと、y=ax+bのaが4ってことだから、あとはその式にxとyを代入して残りのbを求めてみよう
①変化の割合が2で、x=1のときy=5
②xが2増加するとyは4減少し、x=4のときy=-4
すみません!2つともわからないです!できれば早めに教えて欲しいです!(TT)
y=ax+2のグラフが2点(2,3)、(4,b)を通るときa、bの値をそれぞれ求めなさい。
と言う問題で、答えには(2,3)を先に代入すると書いてあったので、(2,3)を代入しました。
すると、y=1/2x+2になり、ここまでは答えとあっていました。
その後に(4,b)を代入するのですが、bに戸惑い計算方法が分かりません。
直線y=-x+1に平行で、直線y=x-5とy軸上で交わる直線
この問題がわかりません
教えてください
>①変化の割合が2で、x=1のときy=5
②xが2増加するとyは4減少し、x=4のときy=-4
1. 一次関数の変化の割合は傾きのこと。
ということはy=2x+bになるはずだから、こいつにxとyの値を代入してbを求めよう。
2. xとyの増加量から変化の割合を求めて、xとyを代入して切片bをゲットしよう。
>y=ax+2のグラフが2点(2,3)、(4,b)を通るときa、bの値をそれぞれ求めなさい。
と言う問題で、答えには(2,3)を先に代入すると書いてあったので、(2,3)を代入しました。
すると、y=1/2x+2になり、ここまでは答えとあっていました。
その後に(4,b)を代入するのですが、bに戸惑い計算方法が分かりません。
たしかにbというと切片とごっちゃになってわかりづらいね。
ここは一旦bを無視して意味だけを考えよう。用は、xが4の時yはどうなるか?ってことがわかればいいんだ。
だからx=4を一次関数に代入して、その時に出てくるyがbになるね
>直線y=-x+1に平行で、直線y=x-5とy軸上で交わる直線
平行ってことは傾きが等しくて、
y軸上で交わるってことは切片が同じってことだ!
一つの面積と一つの座標がわかってる時の解き方がわかりません
>一つの面積と一つの座標がわかってる時の解き方がわかりません
面積からもう1つの座標を出して、
2点の座標から直線の式を計算してみよう
3点A(0,5)B(-1.a+3)C(3,1-a)が
同じ直線上にある時、aの値を求めよ
>3点A(0,5)B(-1.a+3)C(3,1-a)が
同じ直線上にある時、aの値を求めよ
Aは切片だから傾きがあとはわかればaも求められそうだね。
この直線の傾きをcとしてBとCの座標からaとcについての連立方程式を作ってみよう!
y=5分の3x + 5分の21を
3x-5y+21=0の形にする方法を教えてください
すいませんなるべくはやくお願いします♀️
>y=5分の3x + 5分の21を
3x-5y+21=0の形にする方法を教えてください
両辺に分母の5をかけて分数を消し去ろう
分かった!おけ丸!
二つの線が重なっているのを求めるにはどうしたらいいですか?
>二つの線が重なっているのを求めるにはどうしたらいいですか?
2直線の交点の求め方を読んでみて
x-2y=12をy=ax+bの形にするとどうなりますか?
>x-2y=12をy=ax+bの形にするとどうなりますか?
y以外の項を右に移項してみよう。
最後にyの係数で両辺を割ればいい
直線y=2分の1x+10上に点A、直線y=−x+18上に点Bを、ABがx軸に平行になるように取り、B、Aからx軸に垂線を下ろして、長方形ABCD(左上から時計回り)を作る。
点Aは、2直線の交点より下にあるものとする。
長方形ABCDが正方形となるときの点Aの座標を求めなさい。
点AのX座標をaとして、AD=2分の1a+10
AB=(−2分の1a+8)−a←これ!なんでaは引くんですか?長くてすみません
>y=2分の1x+10上に点A、直線y=−x+18上に点Bを、ABがx軸に平行になるように取り、B、Aからx軸に垂線を下ろして、長方形ABCD(左上から時計回り)を作る。
点Aは、2直線の交点より下にあるものとする。
長方形ABCDが正方形となるときの点Aの座標を求めなさい。
点AのX座標をaとして、AD=2分の1a+10
AB=(−2分の1a+8)−a←これ!なんでaは引くんですか?長くてすみません
−2分の1a+8はBのx座標。ABの長さを求めるには、
Bのx座標-Aのx座標
で計算してるからだね
何度もすみません。そのaはなぜ足すのではなく、引くのでしょうか…⁇
図をかいてみるとBはAよりも左にあると思うんだ。
つまり、Bのx座標の方が大きい。だからa(Aのx座標)を引くよ
傾きと座標で求める式でどうやってbを求めるのかわかりません
>傾きと座標で求める式でどうやってbを求めるのかわかりません
傾きがわかってるってことは、
y=3x+b
みたいな感じになってるよね?(傾きが3の場合)
これにx座標とy座標をぶち込んでbの方程式を作ってとけばいいのさ
2点(2,5),(-1,-1)を通る直線がx軸と交わる点の座標を求める問題が分かりません。
教えていただけるとありがたいです!
>2点(2,5),(-1,-1)を通る直線がx軸と交わる点の座標を求める問
まずは直線の式を連立方程式で求めてみよう。
y=ax+bに2つの座標を代入してaとbの連立方程式を作ればいいんだ。
で、その直線の式がもとまったらそいつにy=0を代入して、その時のxの値を求めてみよう
xの増加量が3のとき yの増加量が4で、x=3のとき y=-2である。
これは、どう解けばいいですか!お願いします!
>xの増加量が3のとき yの増加量が4で、x=3のとき y=-2である。
x・yの増加量から変化の割合を計算してみよう。
変化の割合は傾きのことだから、y=ax+bのaがわかることになるね。
あとはその式にxとyを代入してやって残りのbを求めてみよう
点(-2,7)を通り、y=3x-5とy軸上で交わる直線の式を求めなさい。という問題がわかりません!
分かりやすい解き方を教えてつださい!!
お願いします!
>点(-2,7)を通り、y=3x-5とy軸上で交わる直線の式を求めなさい。という問題がわかりません!
まず「y=3x-5とy軸上で交わる」というヒントから、
この直線の式の切片(y=ax+bのbのこと)は-5だろう、ってことが検討つくね。
ってことは、y=ax-5になるから、あとは点(-2,7)を代入して残りのaを求めてやれば直線の式が求められるぜ!
傾きは2によって、(2,0)を通る
っていうのが解説にのっていたのですが、なんで(2,0)を通るのかがわかりません!
それは切片にもよるよな!
傾きだけじゃなくて一次関数の式を丸々求めることが大事
直線3x+4y=15に平行で直線y=2分の3x-6とx軸との交点を通る直線の式を求めなさい
という問題がわかりません
平行ということは傾きが等しい、
x軸と交わるってことは、x軸と交わる座標を通るってことだ
直線y=−x−5とx軸上で交わり、点(3,4)を通る直線の式を求めてください(;_;)
変化の割合とx.yが分かっている一次関数の直線の式の求め方が分かりません
2点(-7.6).(-7.-9)を通る直線の式を教えて下さい!
2点(-7、6).(-7、-9)を通る直線の式を教えてください!
変化の割合が4で,点(2,−5)を通る直線の式を教えてください!
y=―χ+8とy=aχ-1のグラフのaの値を教えてください
こんにちは^^
わかりやすいです!
数学苦手なんで感謝です
(−1、3)、(4、−7)
aとbの連立方程式を解く方法を教えてください!!
直線y=3x−6とy軸上で交わり、傾きが−2の直線
の式が分かりません!
直線y=3x−6とy軸上で交わり、傾きが−2の直線の式が分かりません!教えて下さい!!