解の公式のbが偶数だといいことある??
こんにちは。けんいちだよ。
二次方程式では、便利な「解の公式」を勉強したね。
2次方程式「ax² + bx + c = 0」において、
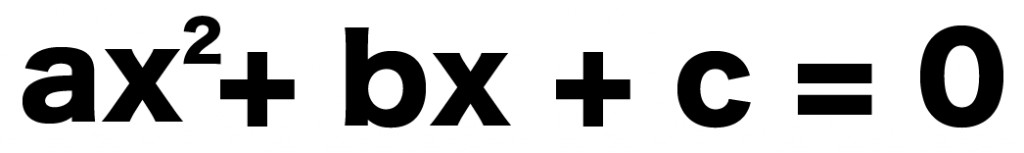
解のxが、
x = {-b±√(b² -4ac)}÷2a
になる公式だったね。
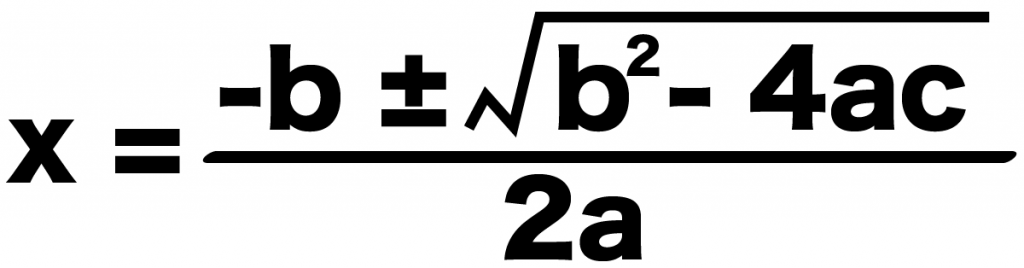
じつはこの解の公式。
なんと、
bが偶数のときは解の公式が使いやすくなるんだ。
b’をxの係数(b)を半分にしたやつとすると、
x = {-b’ ± √(b’²-ac)}/a
たとえば、xの係数が偶数の二次方程式、
x² – 6x +1 = 0
があったとしよう。
このとき、xの係数の半分は-3。
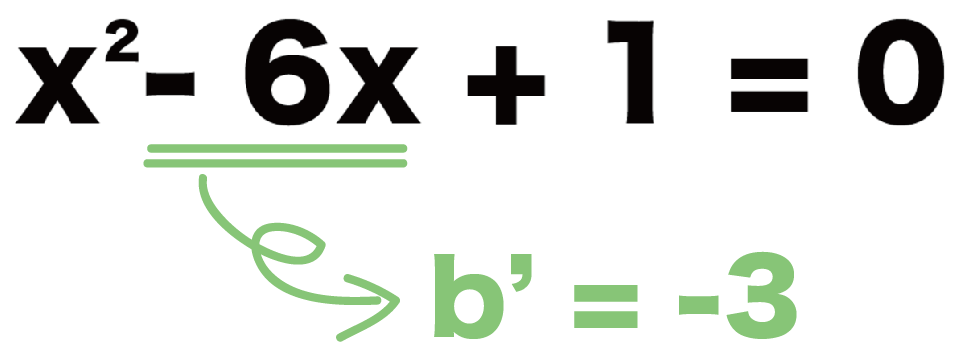
こいつを偶数の公式のb’に代入してやると、
x = {-b’ ± √(b’²-ac)}/a
= {-(-3) ± √(-3)²-1)}/1
= 3± √8
= 3± 2√2
になるね。
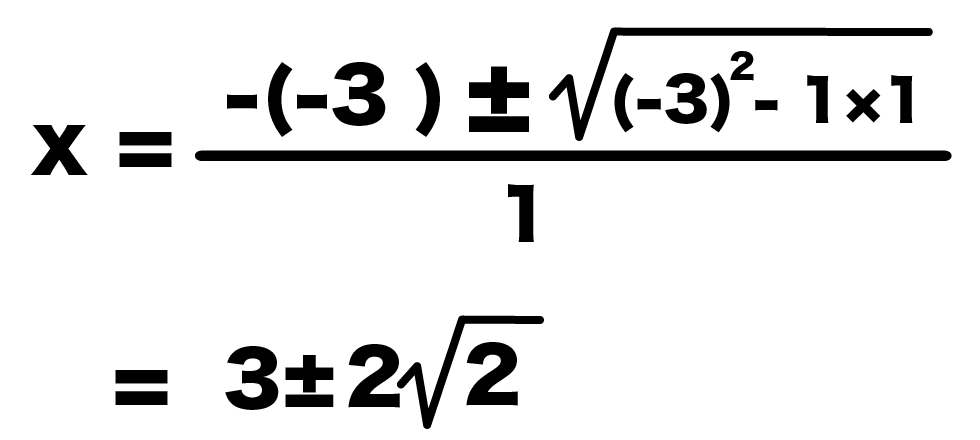
ふつうの解の公式よりも簡単にとける。
まじ最高だ。
今日はせっかくだから、
なぜ偶数の解の公式がつかえるのか??
と
どういうふうに便利になのか??
をみていこうか。
=もくじ=
- なぜ、偶数の解の公式がつかえるの??
- どういうふに便利な公式なの??
なぜ、偶数の解の公式はつかえるの??
bが偶数のときの解の公式は便利ってわかった。
じゃあつぎは、
なぜ偶数のときの解の公式が使えるのか??
をみていこうか。
Step1. bに「2b’」を代入
bは偶数だから、整数b’を使うと、
b=2b’
と表せる。
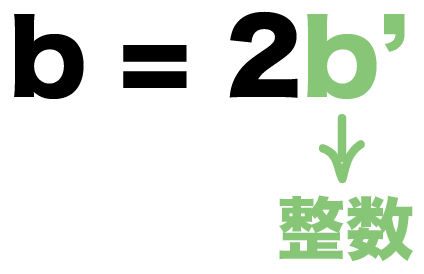
すると、二次方程式「ax² + bx + c = 0」 は、
ax² + 2b’x + c = 0
とかきなおせるね。
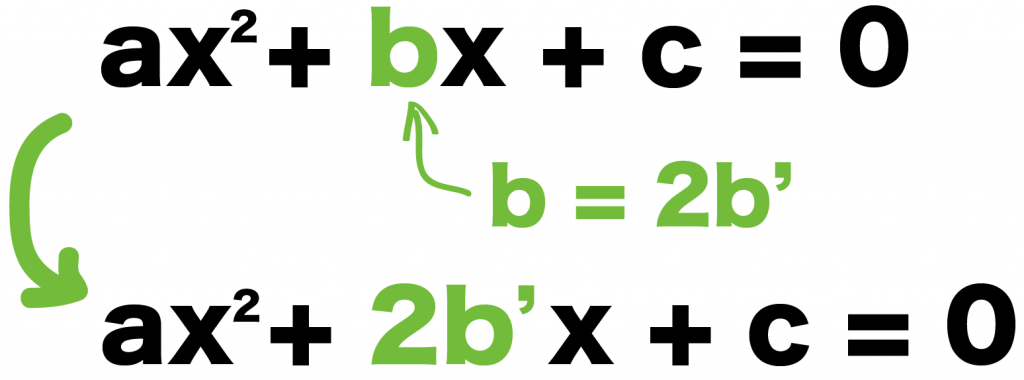
Step2. 解の公式に代入
解の公式のなかの「b」を「2b’」におきかえればいいね。
すると、
x = {-2b’±√((2b’)² -4ac)}÷2a
= {-2b’±√(4b’² -4ac)}÷2a
になる。
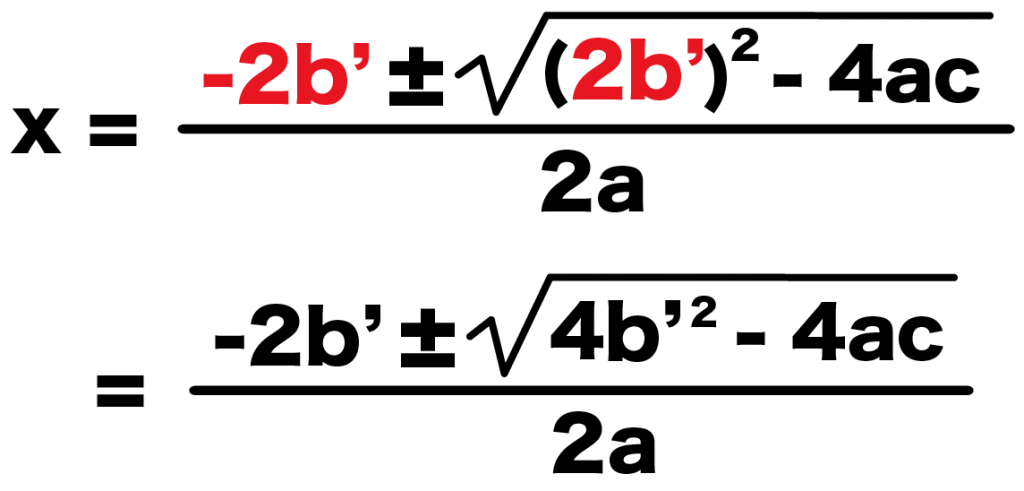
Step3. ルートを簡単にする
つぎはルートの中身を簡単にするよ。
中身の、
4b’² – 4ac
を共通因数の4でくくると、
4( b’² – ac )
になるじゃんね。
4は2の2乗だから、ルートの外にだしてやると、
x = {-2b’±√4(b’² -ac)}÷2a
= {-2b’±2√(b’² -ac)}÷2a
になる。
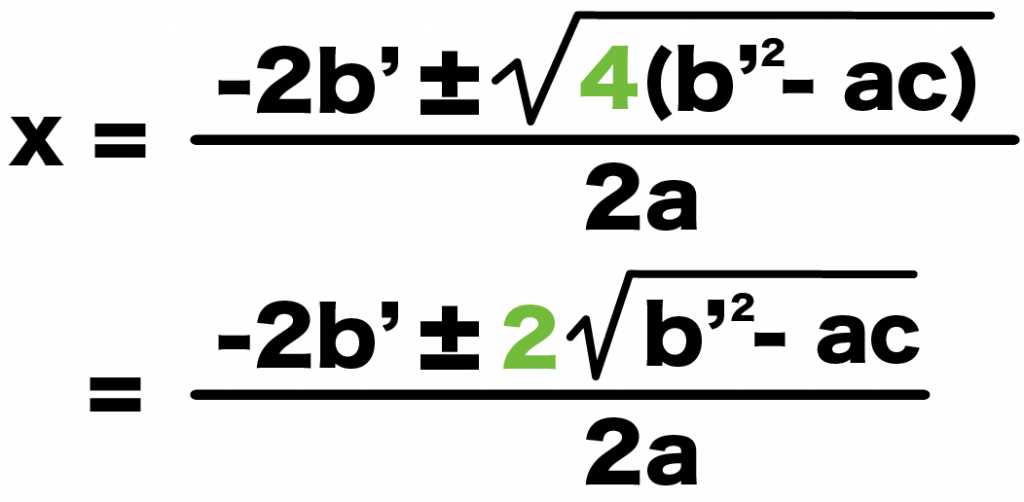
Step4. 約分する
最後に約分しよう。
分母と分子に共通の2っていう約数があるからね。
分母・分子を2でわると、
x = {-b’±√(b’² -ac)}/a
になる。
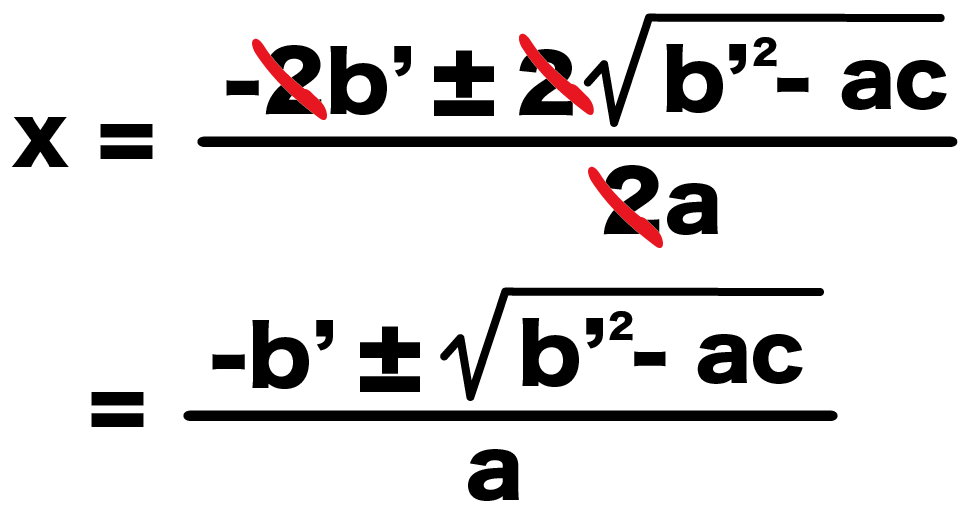
これでbが偶数の公式になったね^^
偶数の解の公式は便利なの??
実際に具体例で計算してみると、それがよく分かるよ。
例えば、2次方程式「3x^2 -8x +1 = 0」をふつうの解の公式で解いてみよう。
係数をそのまま当てはめると、
x = -(-8)±√{(-8)²-4×3×1}/2/3
= 8±2√13/6
= 4±√13/3
になるね。
でも、この二次方程式のbは「-8」で偶数。
さっきの偶数の解の公式もつかえるね。
偶数の解の公式にあてはめてみると、b’=-4だから、
x = -(-4)±√{(-4)²-3×1}/3
= 4±√13/3
ってなるね。
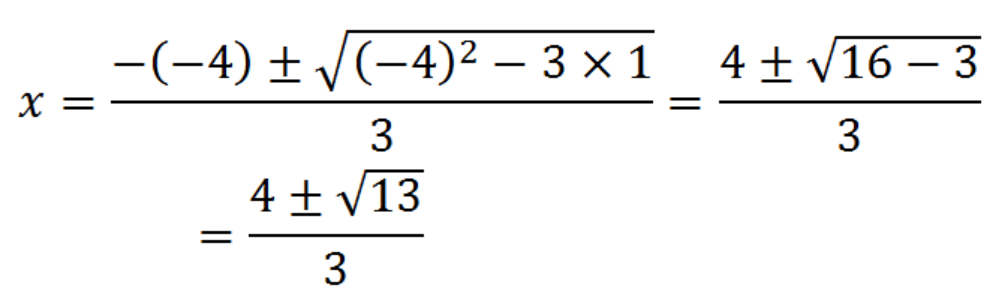
そうそう。
偶数の解の公式をつかってやると、
素因数分解や約分の手間がはぶけるんだ。
a=1のときは分数じゃなくなるからもっと簡単。
bが偶数の場合は絶対お得だよ!!!
まとめ:チャンスがあれば偶数の解の公式をつかおう
二次方程式のbが偶数になってる??
迷わず偶数の解の公式をつかってみよう。
ふつうの解の公式よりはやく解けるからね。
問題をたくさんといてなれていこう。
そんじゃねー
けんいち

公立中学校理科数学講師、進学塾数学講師、自宅塾 高校数学英語化学生物指導、国立大学医学部技官という経歴を持つスーパー講師。よろしくな!

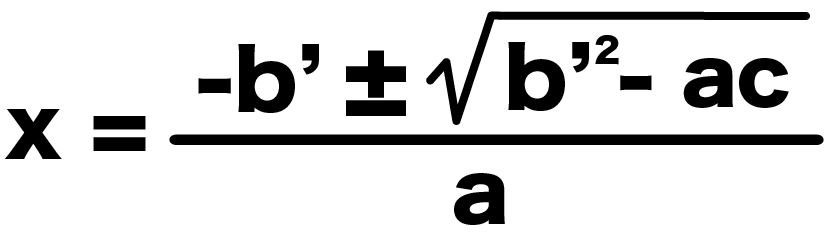
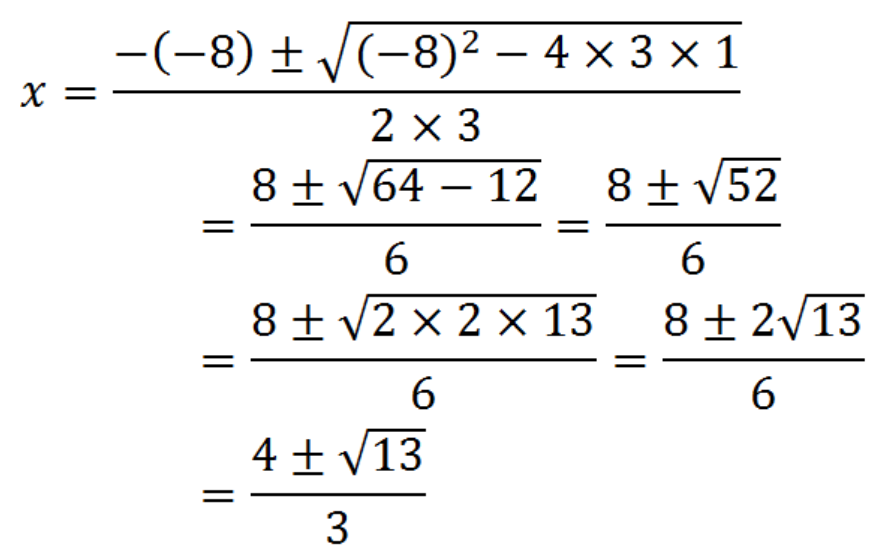




1から200までの数字の中に3の倍数が何個あるかを求める公式?ってありますか?、
つまり、テストでXの係数が偶数の場合は上記のように簡略化された解の公式を絶対に使わなければダメという話ですか?それとも、誤って簡略化される前の解の公式を使ってしまっても、最低限の解答としては、丸を貰えるのでしょうか?
この公式は必須ではありません。単なるショートカット、近道です!
忘れたら元の解の公式を使いましょう。
そして解の公式を忘れたら平方完成でときましょう。
あくまでも大事なのは正解を出すことです。