平行四辺形の対角線の長さの求め方??
こんにちは!この記事をかいているKenだよ。毛布、ほしいね。
平行四辺形の対角線の長さの問題
ってむずい。
でも、
求め方を知っておけば大丈夫。
ドヤ顔で答えられるよ。
たとえばつぎの例題をみてみて。
例題
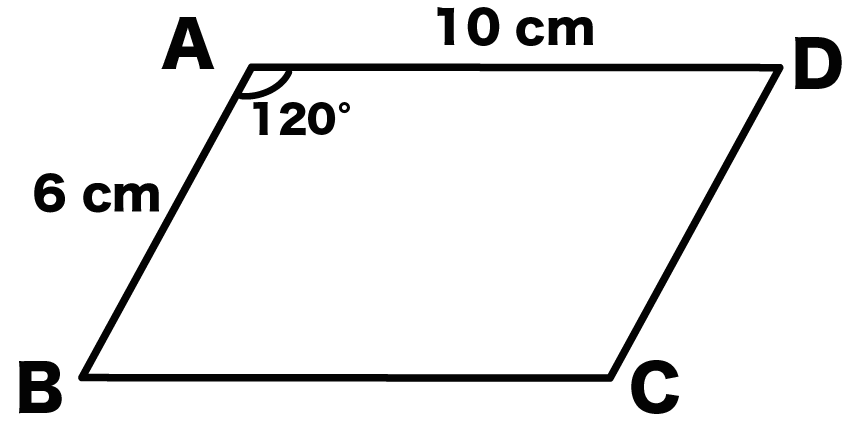
平行四辺形ABCDにおいて、AB = CD = 6cm、AD = BC = 10cmとする。
角A = 120°のとき、対角線ACの長さを求めよ。
今日はこの、
平行四辺形の対角線の長さを求める問題を3ステップで解説していくよ。
よかったら参考にしてみてね。
平行四辺形の対角線の長さの求め方がわかる4ステップ
例題の、
例題
平行四辺形ABCDにおいて、AB = CD = 6cm、AD = BC = 10cmとする。
角A = 120°のとき、対角線ACの長さを求めよ。

をときながら解説していくよ。
つぎの4ステップでとけちゃうんだ。
- 垂線をおろす
- 角度をもとめる
- 高さを求める
- 三平方の定理をつかう
Step1. 「頂点」から垂線をおろす
平行四辺形の頂点から垂線をおろそう。
角度がわかっている頂点から垂線をひいてみて。
例題でいうと、角Aから垂線をひくよ。
だって、
角A = 120°
って角度がわかってるからね。
AからBCに垂線をおろすと、
だいたいこんな感じになる↓↓
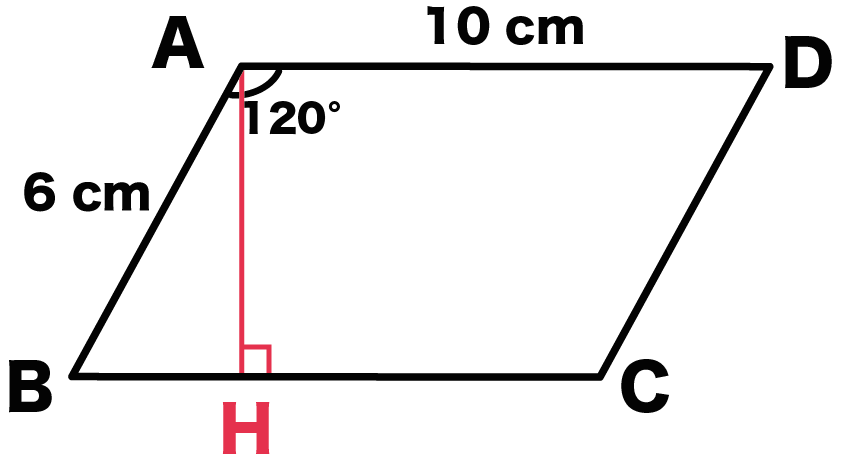
垂線とBCの交点をHとしよう。
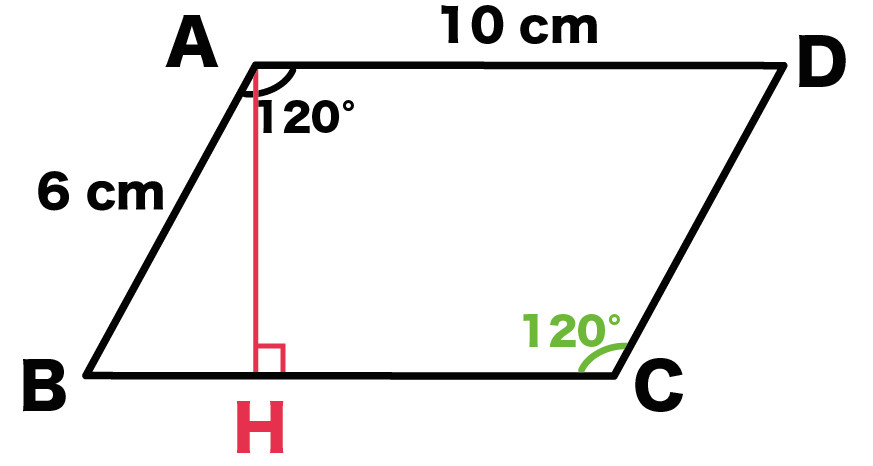
Step2. 平行四辺形の角度を求める
平行四辺形の角度を求めよう。
平行四辺形の性質の、
2組の向かいあう角は、それぞれ等しい
を使うよ。
2組の向かいあう角は、それぞれ等しい
から、
角A = 角C = 120°
ってわかる。
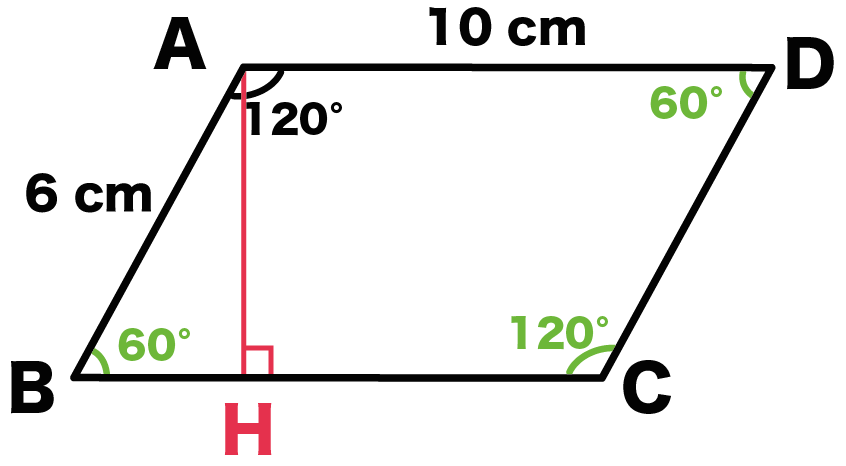
ってことは、
残りの角Bと角Dは、
角B = 角D = (360°- 240°)÷2 = 60°
になるはずだ。
Step3. 平行四辺形の高さを求める
平行四辺形の高さを求めてみよう。
例題でいうと、
線分AHの長さだね。

高さAHの長さを求めるために、
直角三角形ABHに注目してみよう。
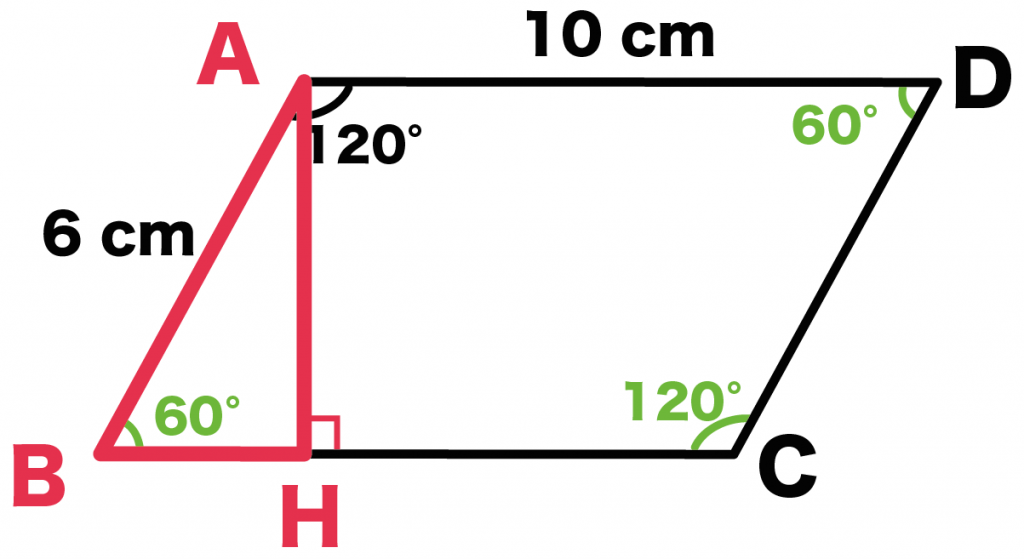
この直角三角形は、
- 角B = 60°
- 角H= 90°
の角度をもっているね。
ってことは、この直角三角形の比は、
1: 2: √3
になるはずだ。
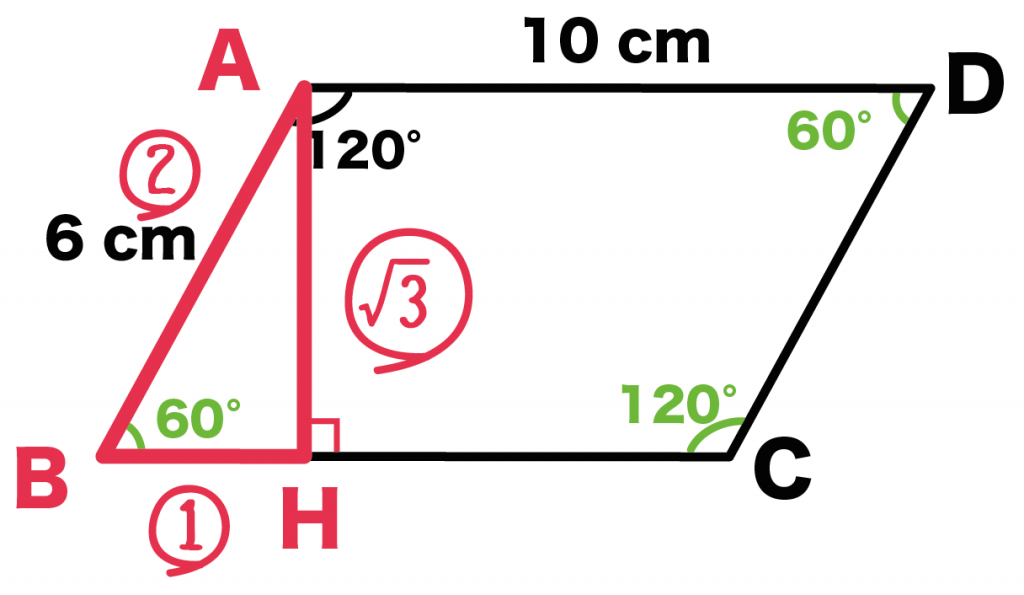
よって、
- AH = 3√3
- BH = 3
になるね。
Step4. 三平方の定理をつかう!
いよいよ最後のステップ。
三平方の定理で「対角線の長さ」をもとめよう!
例題では、
直角三角形ACHに注目してくれ。
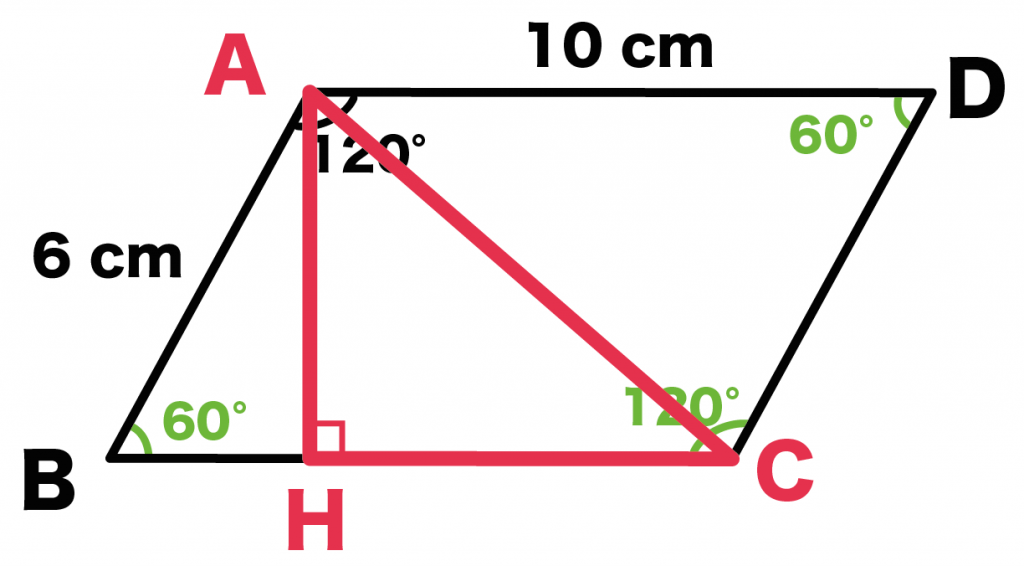
ここでは、
AHとCHで三平方の定理をつかって、
対角線AC の長さを求めていくよ。
Step3より、
- AH = 3√3
- CH = BC – BH = 10-3 = 7
だね。
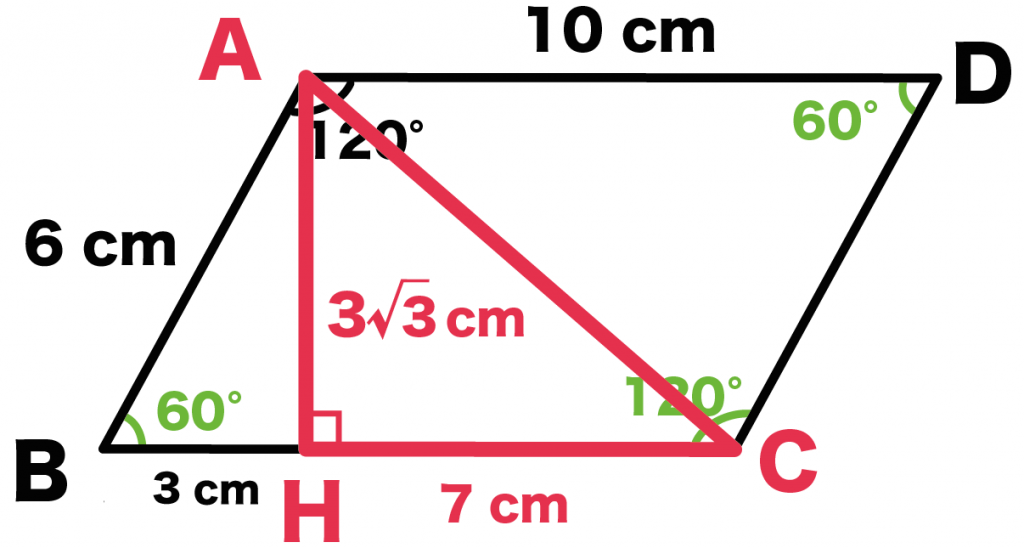
よって、
AC = √(AH^2+CH^2)
= √[(3√3)^2+ 7^2] = 2√19
になる。
おめでとう!
平行四辺形の対角線の長さを計算できたね!
まとめ:平行四辺形の対角線の長さの求め方は直角三角形がカギ
平行四辺形の対角線の求め方はムズい。
だけれども、
直角三角形をうまくつくれば大丈夫。
あとは三平方の定理を使うだけさ。
がんばって計算してみてね^^
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






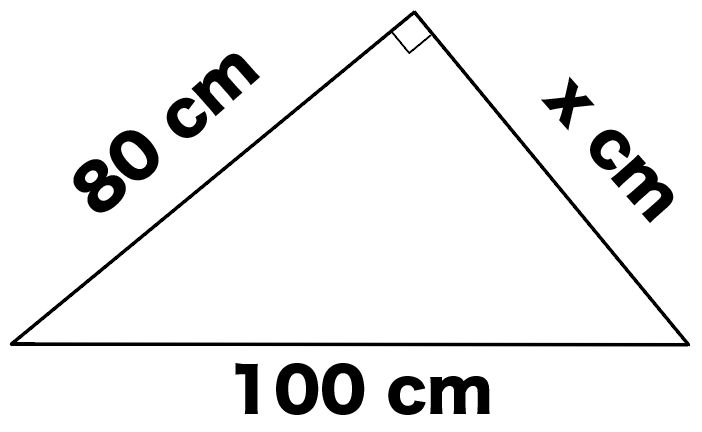
平行四辺形ABCDの返BC上に点Eがあり、線分AEと対角線BDとの交点をFとする。AF=CE,角AFD=90度,AD=5CM,BE=2CMのとき,線分BFの長さは何Cmか?
ECの長さを出す(平行四辺形の性質を使う)
↓↓↓
AFの長さを出す(AF = ECを使う)
↓↓↓
FDの長さを出す(△AFDで三平方の定理)
↓↓↓
BFの長さを出す(△AFDと△EBFの相似比)
でやってみて!
AbイコールAc(対角線)BCイコール8cm BDイコール15cmの平行四辺形があります。
この平行四辺形の面積の求め方を教えてください
なんで1:2:√3が成立しちゃう平行四辺形を例に出しちゃうかな〜安易すぎる