場合の数の調べ方がわからない!
こんにちは!この記事をかいているKenだよ。散歩は大事だね。
中学数学の確率で重要なのは、
場合の数の調べ方
だ。
「場合の数」さえ数えられれば大丈夫。
あとは確率の公式にいれるだけだからね。
「場合の数の調べ方」さえおぼえれば、
確率マスターになれるわけさ。
今日はそんな確率で大切な、
場合の数の調べ方を2つ紹介するよ。
よかったら参考にしてみて。
確率で役立つ場合の数の調べ方2つ
中学数学ではおもに、
樹形図で場合の数を調べていくよ。
調べ方はつぎの2つさ。
- すべての場合の数の調べ方
- あるできごとの場合の数の調べ方
つぎの例題をときながら解説していくよ。
例題
3・4・8がかかれたカードが3枚ある。こいつらを並べて3ケタの数字をつくるとき、偶数になる確率を求めよ。

このとき、樹形図はつぎのようになるね。

※詳しくは「樹形図の書き方」をよんでみてー!
調べ方1. すべての場合の数の調べ方
まずは「すべての場合の数」をしらべよう。
これは確率の計算で分母にくるやつだね。

調べ方はとっても簡単。
樹形図のいちばん右をぜんぶ数えればいいんだ。

例題でいうと、いちばん右には6つの実がなっているよね??
だから、
すべての場合の数は「6通り」になるんだ。
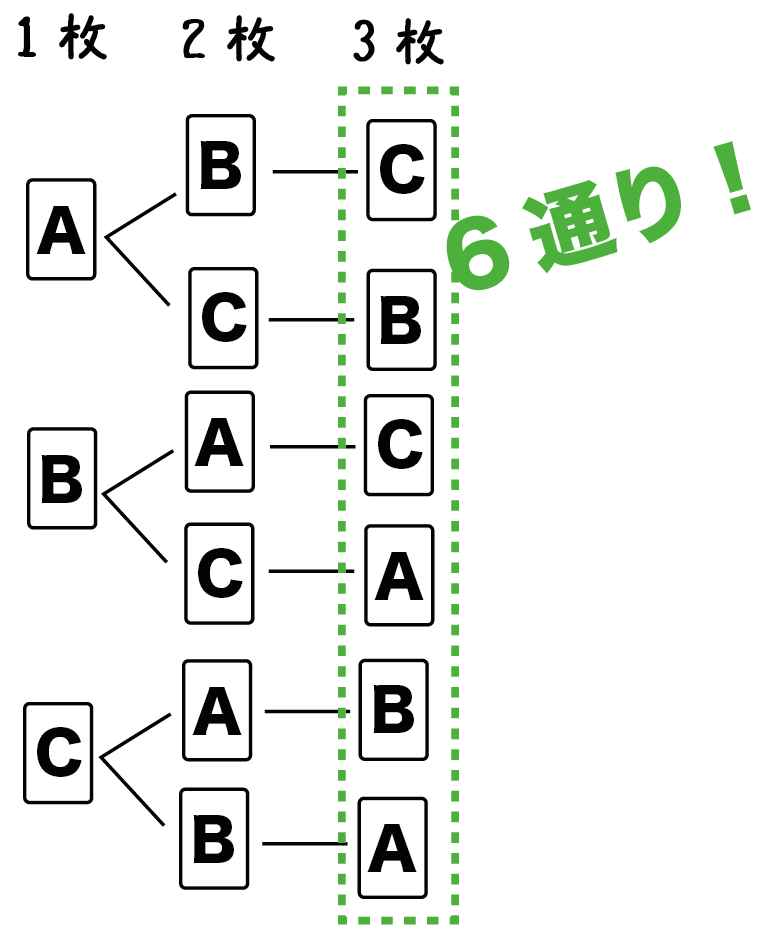
樹形図のいちばん右をかぞえると「すべての場合の数」になる
って覚えておこう。
調べ方2. 「あるできごと」の場合の数の調べ方
今度は「あるできごと」の「場合の数の調べ方」だね。
これは確率の公式の分子にくるやつだ。
この調べ方はちょっとむずかしい。
なぜなら、あてはまる場合の数を樹形図から選ばないといけないからね。
たとえば、さくらんぼが腐ってる場合の数をしらべたいとき。
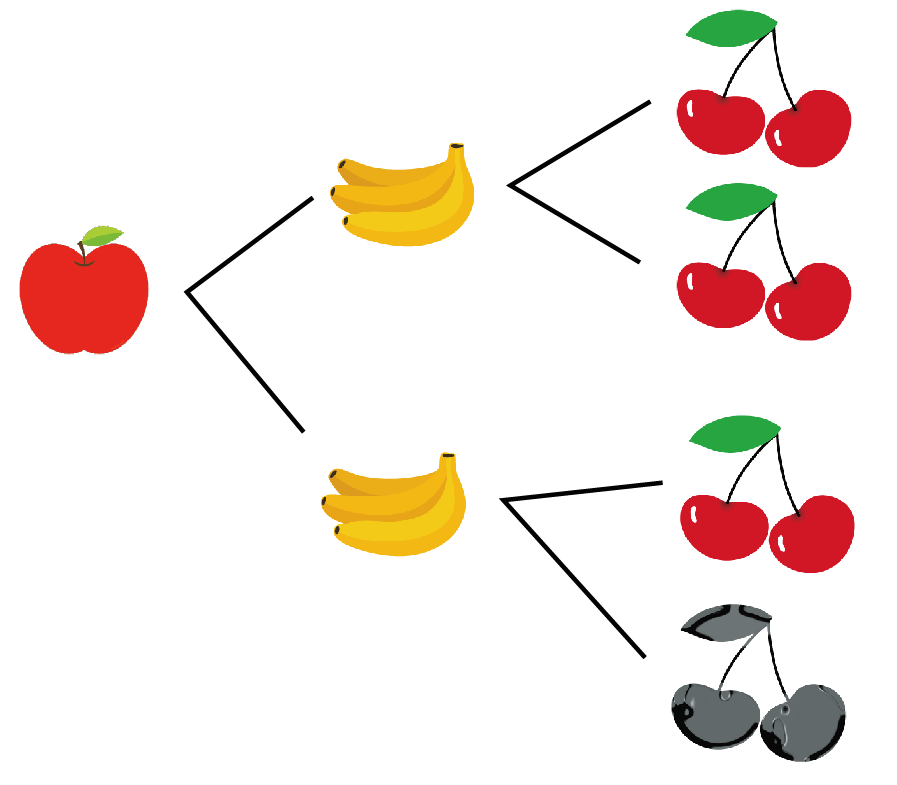
このとき、樹形図をばーーってみてみよう。
さくらんぼが腐ってそうな場合の数をみつけるんだ。
ざっと見た結果、
緑でかこった1通りしかないね。

こんな感じで場合の数を数えればいいんだよ。
例題をみてみよう。
例題で求めたいのは、
3ケタの数字が偶数になる確率
だったよね??
樹形図でかぞえてみると、
4通りある!

よって、
(3ケタの数字が偶数になる確率)
= (偶数になる場合の数)÷(すべての場合の数)
= 4÷6 = 2/3
になるね。

おめでとう!
これで場合の数の調べ方をマスターしたね。
まとめ:場合の数は樹形図と根性で調べよう!
中学数学では基本的に、
樹形図で場合の数をしらべていくよ。
- すべての場合の数
- あるできごとの場合の数
の2つさえ調べられればこっちのもの。
あとは、公式で確率を計算するだけだね。
じゃんじゃん調べていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






当たり3本、はずれ6本が入ったクジから同時に2本引くとき2本とも当たる当たる確率と少なくとも1本外れる確率を求めなさい。という質問の解き方を教えてください
>当たり3本、はずれ6本が入ったクジから同時に2本引くとき2本とも当たる当たる確率と少なくとも1本外れる確率を求めなさい。という質問の解き方を教えてください
くじの確率の問題の記事を読んでみてね。
少なくともの方は、1から2本全部当たりの確率を引けばいいね〜
袋の中から赤玉3つ白玉3つを同時に2つ取り出す時、玉の取り出し方は何通りあるか?
1つ目は6個あるので6通り。
2つ目は5個あるので5通り。
よって6×5=30通りが答えだと思いましたが、正しい答えは15通りでした。
この問題の解き方を教えて下さい。
>袋の中から赤玉3つ白玉3つを同時に2つ取り出す時、玉の取り出し方は何通りあるか?
1つ目は6個あるので6通り。
2つ目は5個あるので5通り。
よって6×5=30通りが答えだと思いましたが、正しい答えは15通りでした。
この問題の解き方を教えて下さい。
これは組み合わせだから最後に被っている数を排除するために2で割ってるんじゃないかな。
赤1白1、白1赤1も同じとしてカウントするからね
0,2,4,6,の4枚のカードがあります。このカードのうち3枚を並べてできる3桁の整数は、全部で何個ですか?
ポイントは0が100の位にくる場合は整数にならないから除外するってことだ
袋の中に、赤玉4個と白玉2個が入っている。この袋の中から球を同時に4個取り出すときに取り出し方が何通りあるかとその時に赤玉3個と白玉1個が取り出されるときの確率について教えてください。
以前、質問させてもらいました、ななしのごんべというものです。
質問をした後によく考えてみたら解くことができました。報告が遅れてしまい申し訳ございませんでした。
なので、以前にした質問の内容は無視してもらって大丈夫です。また、度々お世話になることがあるとおもいます。その時はどうぞよろしくお願い致します 。