比例のグラフってどんな特徴があるの??
こんにちは、この記事を書いているKenだよー!豚角煮カレーおいしかったよ。
前回、「比例グラフの書き方」をみっちり勉強したね?! 比例のグラフをかけるようになったら、あとはテストで点をとり放題・・・・・・
ってわけにはいかないんだ!笑
じつは、比例グラフを自由自在にあやつるためには、
比例のグラフにみられる特徴
を知っておいたほうが有利だ。

比例のグラフともっと仲良くなりたいよね??
今日はもうちょっと深く、「比例のグラフ」について勉強していこう。グラフの特徴を4つ紹介するから勉強の参考にしてみてね^^
比例のグラフにみられる4つの特徴
中1数学で勉強する「比例のグラフ」の特徴は次の4つ。
特徴1. 「原点をとおる」
比例のグラフのいちばん目立つ特徴は、
グラフが原点(0,0)を必ず通る
ってこと。
だから、比例のグラフを書くために原点にポチッと点を打つことが第一ステップなのさ。

それじゃあ、なぜ比例のグラフは原点を通るんだろう??
その答えは比例グラフの式「y = ax」をよーく見てみればわかるよ。
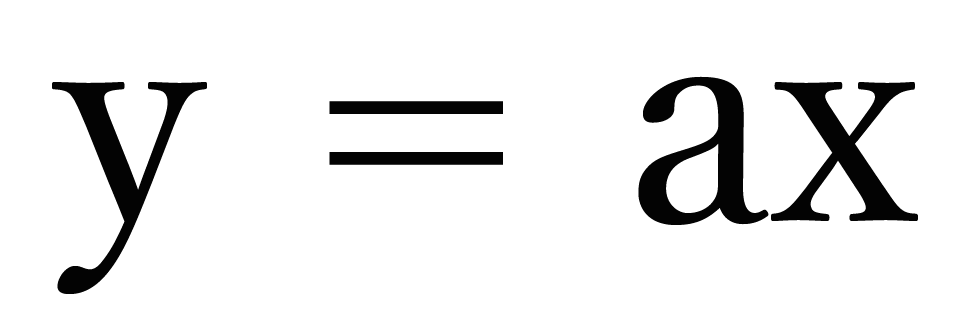
この式のxにゼロをいれてみよう。
すると、yもゼロになるよね?!? xが0のときyも0になる。
つまり、原点(0, 0)を通るってことなんだ。よーく覚えておこう!
特徴2. 比例定数aが大きくなればグラフの傾きが急になる
比例のグラフの2つ目の特徴は、
比例定数aの値が大きくなればなるほどグラフの傾きが急になる
ってこと。たとえば、「y = 2x」と「y = 5x」が座標平面でなかよく暮らしていたとしよう。
この2つの比例の式を書いてみると↓↓

こうなるね!
よーく見てみると、
比例定数aが大きい「y = 5x」のほうが「y = 2x」より急に傾いていることがわかる。
だから、かりに、この2つの比例グラフのうえに「りんご」をのせたら、

こんな感じで、y=5xのりんごのほうがグルグル速く坂をくだっていくはず!笑
比例定数が大きければグラフの傾きが急になる!
ってことを覚えておけば、グラフのカタチを予測できるようになるよ。
特徴3. 比例定数aがプラスのとき・マイナスのときで変化する
もう1つ比例定数に関して押さえておきたいのは、
比例定数aがプラスのときと、マイナスのときでカタチがすっごく違うってこと。
これを確認するために、
y = 2x と y = -2x の比例のグラフを書いてみよう!

aがゼロより大きいとき(プラス)、グラフが右肩あがりになる。
それに対し、
aがゼロより小さいとき(マイナス)、グラフは右肩下がりになってるね。
だから、
かりにりんごを2つの比例の式の上で転がしたら、

りんごが2つとも違う方向に転がりだすでしょ??笑
比例定数aがマイナスのグラフには注意しよう!
特徴4. xの変域の中でしか生きられない
ときどき、比例のグラフの問題で「xの変域」が指定されたものが登場する。
たとえばこんな感じ↓↓
次のグラフを書きなさい。
y = 2x (-2 ≦ x ≦ 2)
このとき、
比例の式に金魚のふんみたいにくっついてる(-2 ≦ x ≦ 2)っていう「xの変域」に注意してくれ。
この変域がついていると、
いつも通りにグラフをばんばん書いちゃいけないんだ。こんな感じでね↓↓

なぜなら、この比例関数には「変域」があるから。
(-2 ≦ x ≦ 2)っていう変域の外にある座標は対応しきれないってことになってる。
だから、この比例の式は、(-2 ≦ x ≦ 2)という範囲だけ元気になるから、

こんな感じで比例の関数が短くなっちゃうんだ。
xの変域が指定されているときは十分に注意しよう!!
まとめ:比例のグラフは意外とシンプル
比例のグラフにたくさんの種類があるけれど、
これら4つの特徴をおさえておけばテストでも大丈夫。
比例グラフがちょっと得意になっているはず笑
そんじゃねー^^
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。

















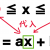











y=3x−3はどうやって
グラフをかけばいいですか?
>y=3x−3はどうやって
グラフをかけばいいですか?
まずは切片を打とう。
あとは、切片からxを1右に進めたら、yが3大きくなる点を打ってみよう。
その2点を結んだら一次関数の出来上がりだ。
詳しくは「一次関数のグラフのかきかた」を読んでみて
ありがとうございました。
とてもわかりやすくてすぐにわかりました。 受験生なので受験がんばります!
ありがとう!頑張ろうぜ!
0.2、0.5
や
1/2、3/8などの書き方がわかりません
教えてください!
>0.2、0.5や1/2、3/8などの書き方がわかりません
教えてください!
比例定数が小数の時は分数に直すといいよ。
分数の時は、原点(0,0)とx分母の数の座標の2点を結べと作図できるよ。
詳しくは「比例のグラフの書き方」を読んでみて
kenさんのQikeruいつも見てます!
私は少しは分かっていたのですが、問題集が全然解けませんでした…
でも、これを見たらわかるようになりました☺️
これからも頑張ってください!
ありがとう!!励みになるよ!!
すいませんえっと反比例の歯車もんだいでAの歯車の数は18で1分間に200回転するモータがついているまたBには色々な数の歯車をつけることができる。という問題でBの歯の数をx1分間の回転数をy回としてyとxの式で表しなさいが訳分からないです。11月の24にテストがあるので教えて欲しいです
塾の問題とかないんです
3:5=×:12解き方教えてください
いいね