エラストテネスの篩(ふるい)で素数を求める??
こんにちは!この記事をかいているKenだよ。中華は鉄板だね。
素数は何かってなんとなくわかった。
だけど、
どうやって素数を求めればいいんだろう??
正直、求め方がわからない。
勘?? 運?? 電卓??・・・
じつは素数の求め方の1つに、
エラトステネスのふるい(篩)
っていう方法があるんだ。
ちょっと正直、ひびきがうさんくさいね笑
だけど、使い方をおぼえるとチョー便利だから、
「エラストテネスのふるい」を5ステップでつかってみよう。
これをマスターすれば大丈夫。
素数を1発で求められるよ!
エラストテネスのふるい(篩)の使い方がわかる5ステップ
5ステップで素数を求めていくよ。
- 自然数をかく
- はじめらへんの素数に○をつける
- 「1」を斜線で消す
- 「○をつけた素数の倍数」を斜線で消す
- 残ったやつが「素数」
例として、
を求めてみよう!
Step1. 自然数をかきまくる
求めたい範囲の自然数をかいてみよう。
今回でいうと、
1から100までの素数を求めたい
んだったね??
だから、1から100までの自然数をかけばいいのさ。
えっ。
自然数のかきかたがわからんって??
そうだね。
1行あたりに10個の自然数をかいてみて。
ちょうどこんな感じ↓↓
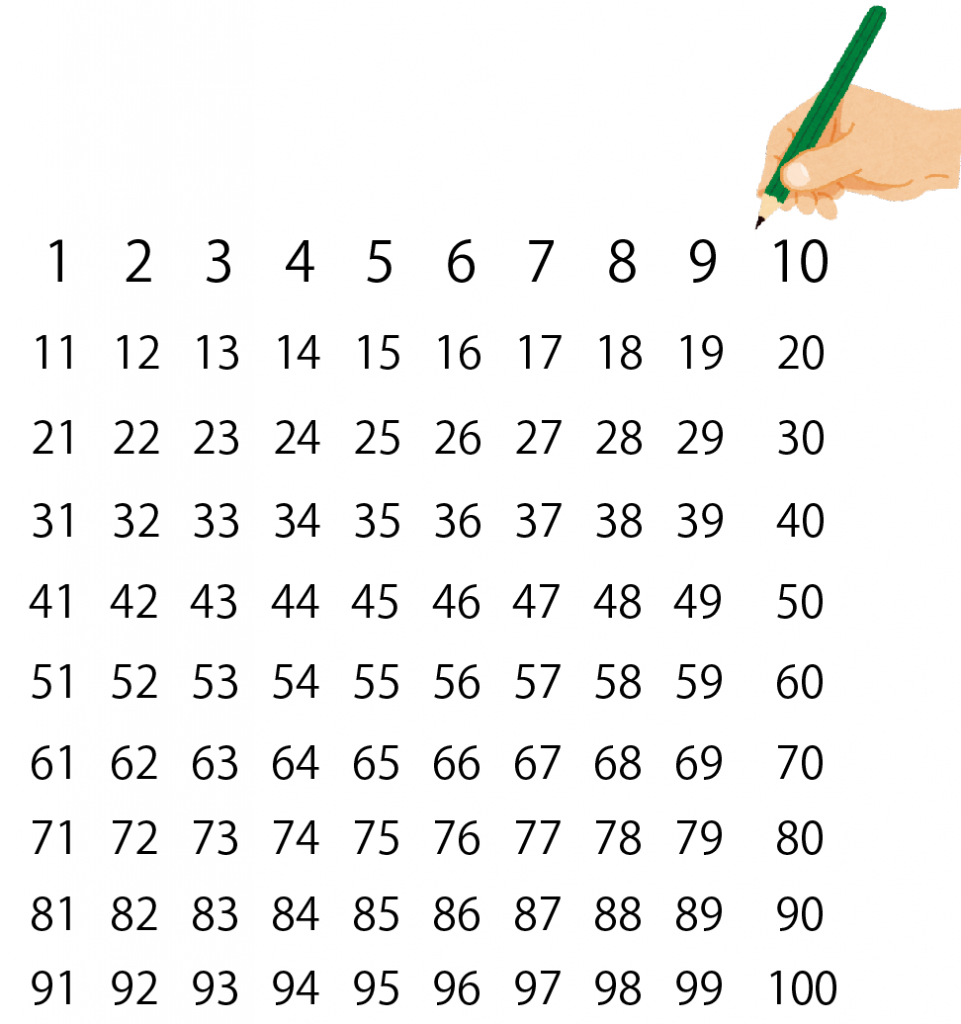
手が疲れるかもしないけど、ここが一番きついとこ。
歯をくしいばって自然数をかいてみよう。
Step2. 最初のほうの素数に○をつける
最初のほうの素数に○をつけよう。
えっ。
どこまでの素数に○つければいいのかって??
じつは、
2乗しても範囲をこえない素数
まで○でかこえばいいんだ。
1から100までの自然数にふくまれる素数だったら、
範囲でいちばん大きいのは100でしょ??
2乗しても100をこえない最大の素数は「7」だね。
なぜなら、つぎの素数の「11」は2乗すると「121」になるからね。
100をこえちゃう。
だから、7までの素数の、
- 2
- 3
- 5
- 7
の4つを○でかこうんだ。

これが第2ステップ!
Step3. 「1」を斜線でけす
左上の「1」を斜線でけそう。
赤でも緑でも構わない。
とにかく、消してやろう。

1は素数じゃないから消すんだ。
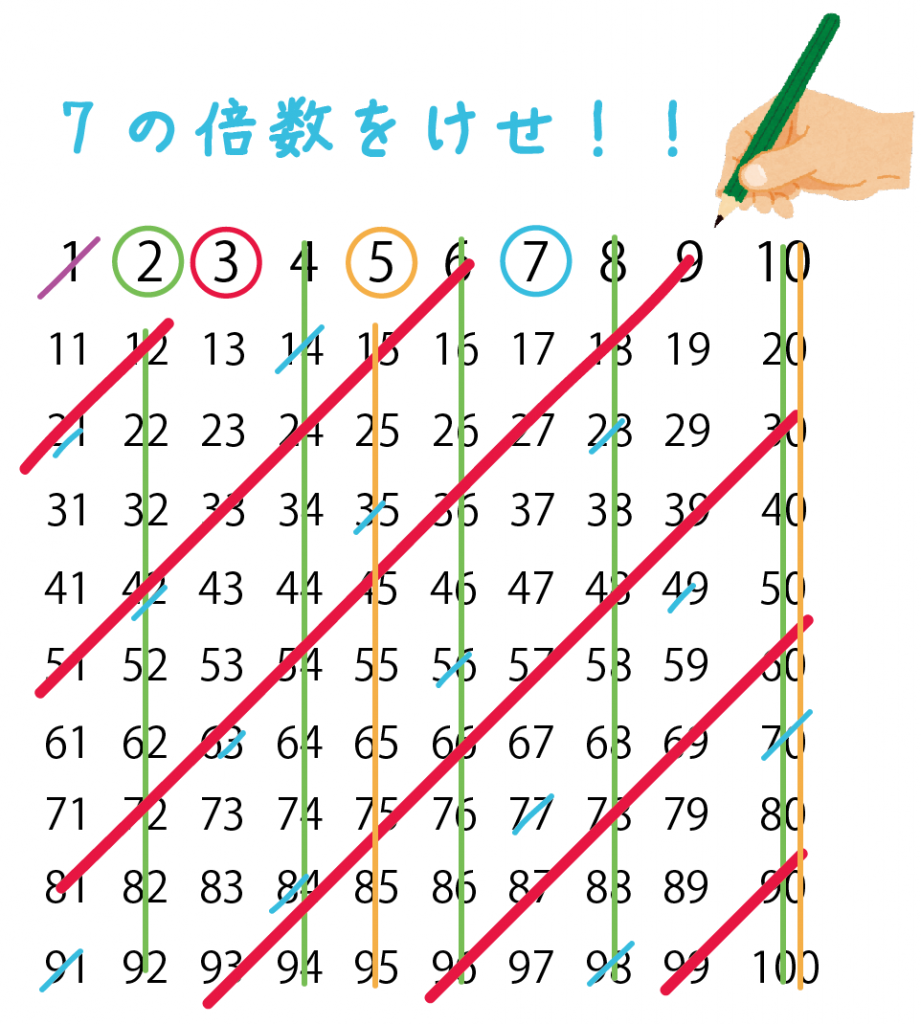
Step4. ○つけた素数の倍数をけす!
今度は○がついてる素数の倍数をけすよ。
なぜなら、
「素数の倍数」は素数じゃないからね。
「1」と「自分」以外でも割れちゃうようになるもん。
例題でいうと、まず「2」の倍数をけしてやる。
偶数をぜーんぶ消すんだ。

おつぎは3の倍数。
斜めにしゅーっと線をひいてあげよう。

つぎは5の倍数。
5の倍数は、
- 1の位が「5」
- 1の位が「0」
の2通りになるはず。
だから「5」と「10」の下の数字たちはみーんな消されちゃう。

最後に7の倍数。
100以下で7の倍数になっている、
- 7
- 14
- 21
- 28
- 35
- 42
- 49
- 56
- 63
- 70
- 77
- 84
- 91
- 98
をけしてやろう!
Step5. 残った数を○でかこう
最後まで生き残った自然数を○でかこってみて。
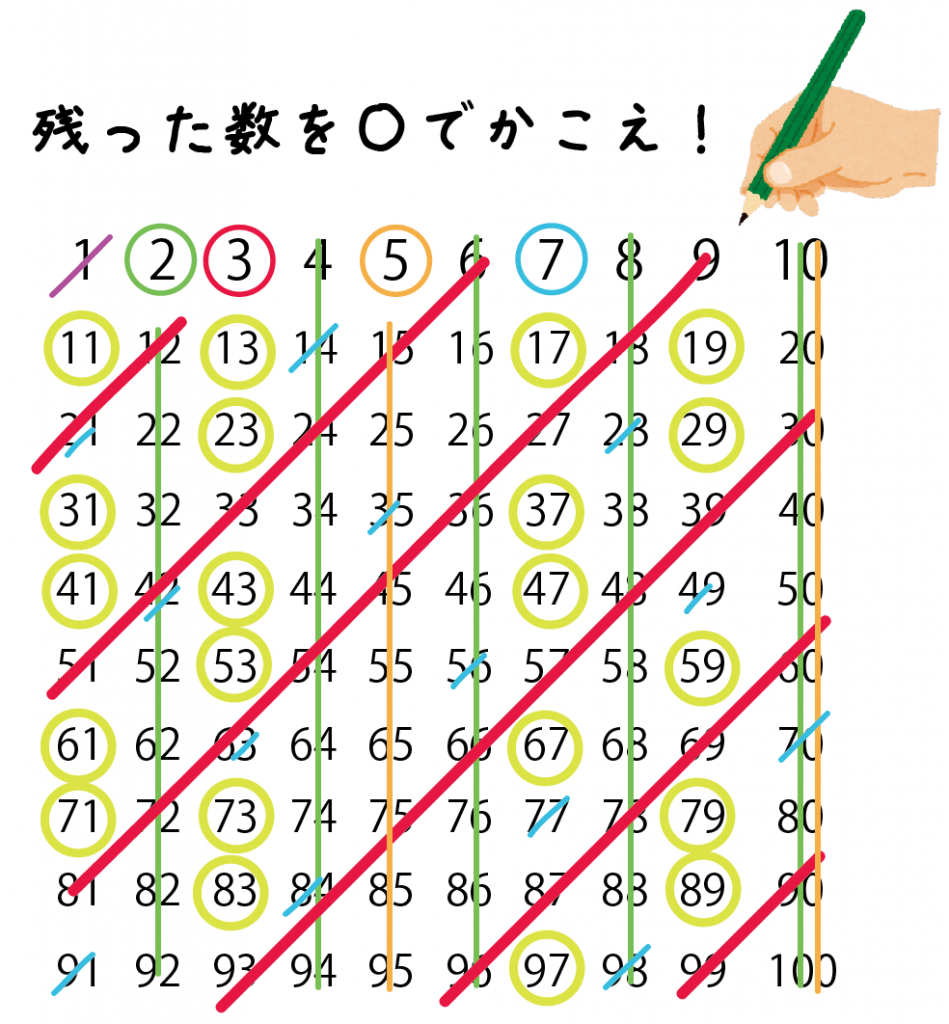
○がついたぜーんぶの自然数が、
素数
だ。
どう? 案外簡単でしょ??
まとめ:エラストテネスの篩(ふるい)はあとから楽になる
エラストテネスの篩はちょー便利。
簡単でわかりやすい。
ただ、ちょっと残念なのが、
最初に自然数をたくさんかくところだ。
もし、1から1000までの素数を求めなきゃいけなかったら、
1000個の自然数をかかなきゃいけない。ゼッタイに手が震えるね。
でも、最初さえ乗り切れればあとは楽になる。
エラストテネスのふるいでガンガン素数を求めていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






こんにちは。私は今中学三年生です。そろそろ受験勉強をしないといけない頃だなーと感じています。
私は特に数学が苦手です。何か良い勉強法があればぜひ教えてください。
もし良ければ英語の勉強法も教えてください。
>私は特に数学が苦手です。何か良い勉強法があればぜひ教えてください。
数学は、
知識の吸収→問題演習→復習
のサイクルをいかに多くこなせるかが重要。
基礎を抑えたらたくさん問題を解いて、間違えた問題を復習してみよう。
>もし良ければ英語の勉強法も教えてください。
英語は単語力と文法の理解が大事だね。
受験だと長文問題がメインになるから、今から簡単な英語の長文を読む練習をしておくといいかな
もっと簡単な素数の求め方
教えて
素数の見つけ方ってほかにはありますか?
エラストテネス?エラトステネスじゃない?
エラトステネスだと思うんだが……
エラトステネスだったはずだよん!