共通因数とはなんだろう??
こんにちは!この記事をかいているKenだよ。豆乳にはハチミツだね。
因数分解の基本ワザに、
共通因数でくくる
があるよ。
これは基本中の基本。
柔道でいうと背負い投げ。
空手でいうとかわら割りかもしれない。
今日はそんな因数分解の基本の、
共通因数のくくり方を4ステップで解説してみたよ。
よかったら参考にしてみて。
=もくじ=
- そもそも共通因数とはなにもの?
- 共通因数のくくり方がわかる4ステップ
そもそも共通因数とはなにもの??
共通因数とは、
2つ以上の項に含まれるおなじ因数のこと
なんだ。
たとえば、
6 + 8
っていう多項式があったとしよう。

この、
- 6
- 8
の項に注目してほしい。
こいつらの共通因数は「2」だ。
なぜなら、2つの自然数を素因数分解してみると、
- 6 = 2×3
- 8=2×2×2
になってて、共通する因数は「2」だからね。

どう??
しっくりきたかな??
共通因数のくくり方がわかる4つのステップ
共通因数のくくり方は4ステップでいけちゃうよ。
- 各項を因数分解
- 共通因数をみつける
- 共通因数をとり出して()をつける
- 元に戻す
例として、
9a²b³ – 21b²
から共通因数をとりだしてみよう!

Step1. かるく因数分解
まず、各項をかるく因数分解してみよう。
係数は素因数分解して、
文字は指数をばらせばいいんだ。

例題でもかるーく因数分解してみると、
- 9a²b³ = 3×3×a×a×b×b×b
- – 21b² = -(3×7×b×b)
になるね。

これが第1ステップ。
Step2. 共通因数をみつける
つぎは、因数から共通のものをみつけよう。
例題では、
3×b×b
が共通因数っぽいね!
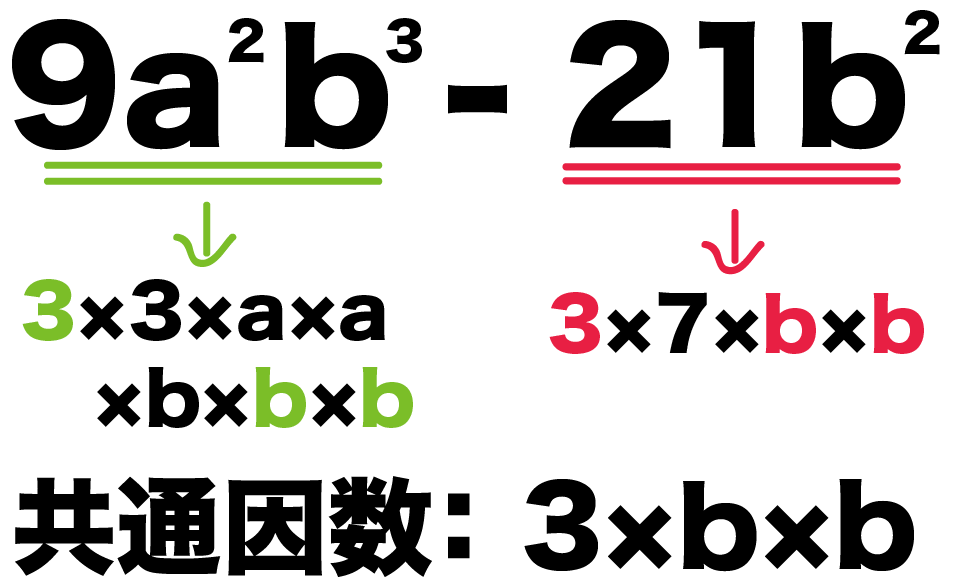
だって、2つの項に共通してふくまれてるし。
もれなく数や文字をカウントしよう!
Step3. 共通因数をとり出して()でくくる
共通因数を項からとり出してみよう。
ただ取り出すだけじゃない。
ついでに()でくくらなきゃいけないね。
共通因数「3×b×b」をとり出して()でくくると、

3×b×b ( 3×a×a×b – 7)
になるね。
Step4. かけ算を元に戻す
最後はかけ算を元にもどすだけ。
例題でかけ算をなくしてやると、
3×b×b ( 3×a×a×b – 7)
= 3b²(3a² b-7)
になるはずだ。

おめでとう!
無事に共通因数でくくれたね^^
まとめ:共通因数はかるく因数分解してみつけよう!
共通因数のくくり方はどうだったかな??
項をかるーく因数分解して、共通の因数をみつければいいんだ。
くくりだして問題になれていこう!
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。






















n-2(n-1)が計算できません。
分配法則で()を展開してみよう!
x(y-z)-y+zの-y+zでくくる場合を教えて頂けるとありがたいです
そしたらx(y-z)にマイナスの符号をつけてやればいいね。
-x(-y+z)-y+z
って感じで
-5b^+2abという式は共通因数bでくくらなきゃいけないんですか?
>-5b^+2abという式は共通因数bでくくらなきゃいけないんですか?
そのままでもいいよ
くくりだした数字や文字はどうなるの?
いや、まだ生きてるよ
(x-1)(x+2) 共通因数(x-1)でくくる -> (x+2) となるのですが どういう 意味か わかりません。
お願いします 誰か助けてください
>(x-1)(x+2) 共通因数(x-1)でくくる -> (x+2)
ちょっとよくわからない汗
仮に、
(x-1)(x+2)+(x-1)
だったら、
(x-1)(x+2)+(x-1)
= (x-1)(x+2+1)
= (x-1)(x+3)
になるけどね
方程式の時にはそのまま約分はだめなんですか??
y=2x+2
→y=x+1
のような感じです!
>方程式の時にはそのまま約分はだめなんですか??
y=2x+2
→y=x+1
のような感じです!
惜しい!それだと右辺しか2で割ってないから等式は成り立たない!
やるんだったら両辺とも同じ数で割ってあげる必要がある。
例えば、
2y=2x+2
→y=x+1
(両辺を2で割ってる)
問題に分数がでてきてわからないです…
>問題に分数がでてきてわからないです…
一旦、分母は無視して分子だけで共通因数をくくってみよう
X二乗ー3分の1Xー8=0
の解き方を教えてください。
>X二乗ー3分の1Xー8=0
両辺に3をかけて分数を消し去ろう。
そしたら、たすき掛けの因数分解を使ってみよう
(k^2+k/2)^2+(k+1)^3の共通因数の見つけ方が分かりません
(a-b)p-q(b-a)^2=(a-b)p-q(a-b)^2に
なる理由が分かりません
>(a-b)p-q(b-a)^2=(a-b)p-q(a-b)^2に
なる理由が分かりません
(b-a)を2乗しても、それにマイナスをかけた(a-b)を2乗しても、
2乗すると正の数になるから同じになるんだろうね
1/2m{2a+(m−1)d}−1/2n{2a+(n−1)d}=0
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
→ 1/2(m−n){2a+(m+n−1)d}=0
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
なぜこうなるのですか?2段目の()の中身が分かりません
>1/2m{2a+(m−1)d}−1/2n{2a+(n−1)d}=0
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
→ 1/2(m−n){2a+(m+n−1)d}=0
1/2m{2a+(m+n−1)d}−1/2n{2a+(m+n−1)d}=0
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
だったらそうなりそうなんだけどなあ
ab(x -y)+a(y -x)の解き方を教えてください
>ab(x -y)+a(y -x)の解き方を教えてください
これは置き換えの因数分解の問題だね。
A = x-y
としてみようぜ
2ab^2-3ab-2a+b-2
=(b-2)(2b+1)a+(b-2)
=(b-2){(2b+1)a+1}
↑
なぜ(b-2)でくくったのに+1が残るのですか?
教えてください
>2ab^2-3ab-2a+b-2
=(b-2)(2b+1)a+(b-2)
=(b-2){(2b+1)a+1}
↑
なぜ(b-2)でくくったのに+1が残るのですか?
教えてください
b-2 = Bと置き換えてみるとわかりやすいね!
8x³y³-10x²y
=2x²y(4y²-5)
↑の式の途中式がわかりません。
教えてください。
>8x³y³-10x²y
=2x²y(4y²-5)
これは分配法則を知っていればわかるね!
因数分解の工夫で、たすき掛けを利用する問題があり、共通因数のくくりだしで、5xyとー5xをくくって5x(y-1
)にしてしまうと、たすき掛けの答えがどうしてもあわなくなってしまいます。
x(5y-5)だと答えがあうのですが、係数の5はくくりだしてはいけないのでしょうか。
>因数分解の工夫で、たすき掛けを利用する問題があり、共通因数のくくりだしで、5xyとー5xをくくって5x(y-1
)にしてしまうと、たすき掛けの答えがどうしてもあわなくなってしまいます。
x(5y-5)だと答えがあうのですが、係数の5はくくりだしてはいけないのでしょうか。
x(5y-5)にするのはxの係数を(5y-5)だとわかりやすいからたすき掛けが使えたんだろうね!
5x(y-1)でもいいけど、その場合のxの係数は()のなかのy-1じゃなくて外の5を含めた5(y-1)になる
-(3×7×b×b)のかっこを取る時、-3×-7×-b×-bにならないのは何故ですか?この時はマイナスは分配法則しないんですか?
>-(3×7×b×b)のかっこを取る時、-3×-7×-b×-bにならないのは何故ですか?この時はマイナスは分配法則しないんですか?
分配法則は()の中にある複数の項に外の数をかけていくからね。
で、項ってやつは+でつながってるやつであって×で繋がってるわけではない。
この場合、()の中の項は3×7×b×bの1つになるね
すみません、最後の()でくくった式はそこから分配法則を使ってまとめるのですかね?
それとも、()でくくった式で既に因数分解出来ているということですか?
モヤモヤして夜も眠れない(バリバリ眠れてる<殴)ので教えてください!お願いします!
()でくくった式で既に因数分解出来ているね!
64X2乗−16X+1の因数分解
正解は (8X−1)2乗 ですが、(−8X+1)2乗 も正解ですか?
正解だね!ただ (8X−1)2乗の方が美しい